Calculate the electric field due to a dipole on its axial line and equatorial plane. Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Electric field due to an electric dipole at points on the axial line. Consider an electric dipole placed on the x-ax is as shown in figure. A point C is located at a distance of r from the midpoint O of the dipole along the axial line,.

$\to E = \frac{1}{4 π ε_{0}} \frac{q}{{(r - a)}^{2}}$ along BC
since the electric dipole moment vector $\to p$ is from -q to +q and is directed along BC, the above equation is rewritten as
${\to E}_{+} = \frac{1}{4 π ɛ_{0}} \frac{q}{{(r - a)}^{2}} ˆ p$ ........(1)
$\to E = \frac{1}{4 π ɛ_{0}} \frac{q}{{(r - a)}^{2}} ˆ p$ ...........(2)
where $ˆ p$ is located closer to the point C than $- q, {\to E}_{-} . {\to E}_{+}$ us stronger than ${\to E}_{-}$ . therefore the length of the ${\to E}_{+}$ vector is drawn large than that of ${\to E}_{-}$ vector.
The total electric field at point C is calculated using the superposition of the electric field
${\to E}_{tot} = {\to E}_{+} + {\to E}_{-}$ .............(3)
$= \frac{1}{4 π ɛ_{0}} \frac{q}{{(r - a)}^{2}} ˆ p - \frac{1}{4 π ɛ_{0}} \frac{q}{{(r - a)}^{2}} ˆ p \Rightarrow {\to E}_{tot} = \frac{1}{4 π ɛ_{0}} (\frac{1}{{(r - a)}^{2}} - \frac{1}{{(r + a)}^{2}}) ˆ p$ ............(4)
${\to E}_{tot} = \frac{1}{4 π ɛ_{0}} q (\frac{4 r a}{{(r^{2} - a^{2})}^{2}}) ˆ p$ ..............(5)
Note that total electric field is along ${\to E}_{+}$ since +q is closer to C than -q.

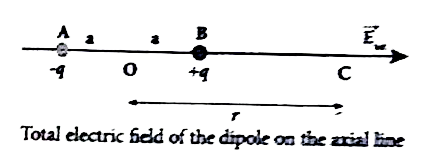
The direction of ${\to E}_{tot}$ is shown in figure
If the point C is very far away from the dipole then $(r > > a)$ .
Under this limit the term ${(r^{2} - a^{2})}^{2} \approx r^{4}$ Substituting this into equation we get
${\to E}_{tot} = \frac{1}{4 π ɛ_{0}} (\frac{4 a q}{r^{3}}) ˆ p (r > > a)$
since 2aq $ˆ p = \to p$
${\to E}_{tot} \frac{1}{4 π ɛ_{0}} \frac{2 \to p}{r^{3}} (r > > a)$
If the C is chosen on the left side of the dipole the total electric field is still in the direction of $\to p$ .
Case (ii) Electric field due to an electric dipole at a point on the equatorial plane
Consider a point C at a distance r from the midpoint O of the dipole on the equatorial plane as shown in figure. since the point C is equi-distance from +q and -q , the magnitude of the electric field of +q and -q are the same. The direction of ${\to E}_{+}$ is along BC and the direction of ${\to E}_{-}$ is along CA.
${\to E}_{+} and {\to E}_{-}$ are resolved into two components one component parallel to the dipole axis and the other perpendicular to it . The perpendicular components $∣ ∣ {\to E}_{-} ∣ ∣ sin θ and ∣ ∣ {\to E}_{-} ∣ ∣ sin θ$ are oppositely directed and cancel each other. The magnitude of the total electric field at point C is
the sum of the parallel components of ${\to E}_{+} and {\to E}_{-}$ and its direction is along $- ˆ p$ .
${\to E}_{tot} = - ∣ ∣ {\to E}_{+} ∣ ∣ cos θ ˆ p - ∣ ∣ {\to E}_{-} ∣ ∣ cos θ ˆ p$ ........(1)
The magnitude ${\to E}_{+} and {\to E}_{-}$ are the same and are given by
$∣ ∣ {\to E}_{+} ∣ ∣ = ∣ ∣ {\to E}_{-} ∣ ∣ = \frac{1}{4 π ɛ_{0}} \frac{q}{(r^{2} + a^{2})}$ ..............(2)

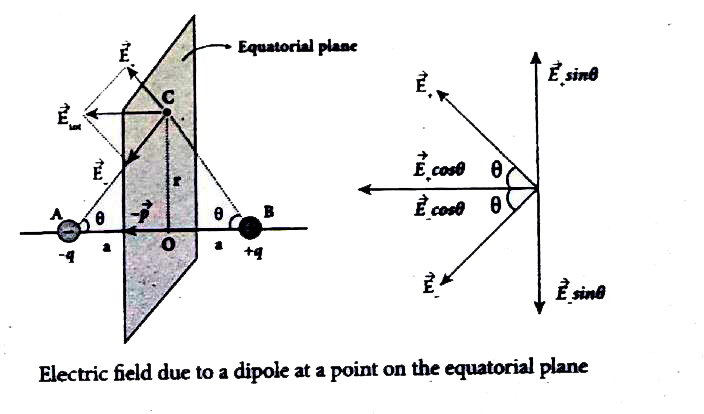
By substituting equation (1) into equation (2) ,we get
${\to E}_{tot} = - \frac{1}{4 π ɛ_{0}} \frac{2 q cos θ}{(r^{2} + a^{2})} ˆ p = - \frac{1}{4 π ɛ_{0}} \frac{2 q a}{{(r^{2} + a^{2})}^{\frac{3}{2}}} ˆ p$ sinc $cos θ = \frac{a}{\sqrt{r^{2} + a^{2}}}$
${\to E}_{tot} = - \frac{1}{4 π ɛ_{0}} \frac{\to p}{{(r^{2} + a^{2})}^{\frac{3}{2}}}$ since $\to p = 2 q a ˆ p$ ............(3)
At very large distance $(r > > a)$ the equation becomes
${\to E}_{tot} = - \frac{1}{4 π ɛ_{0}} \frac{p}{r^{3}} (r > > a)$ ............(4)

|

Updated on:21/07/2023

Class 12 PHYSICS SAMPLE PAPER -4 (SOLVED)

Topper's Solved these Questions

Similar Questions

FULL MARKS-SAMPLE PAPER -4 (SOLVED)-PART-IV

Home
Ask Doubt
Profile