Calculate the electric field due to a dipole on its axial line and equatorial plane.
Case (i) Electric field due to an electric dipole at points on the axial line . Consider an electric dipole placed on the x-ax is as shown in figure . A point Cis located at a distance fo r from the midpoint O of the dipole along the axial line . The electric field at a point C due to + q is
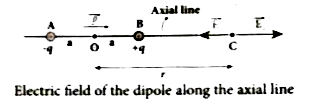
→E=14πε0q(r−a)2 along BC
Since the electric dipole mometn vector →p is from -q is from -q to +q and is drected along BC the above equation is rewritten as
→E+=14πε0q(r−a)2ˆp
where ˆp is the electric dipole moment unit vector from -q to +q . The electric field at a point C due to -q is
→E−=−14πε0q(r+a)2ˆp
Since +q is located closer to the point C than -q , →E−.→E+ us stronger than →E . Therefore the length of the →E+ vector is drawn large than that of →E− vector .
The total electric field at point C is calculate using the superposition principle of the electric field .
→Etot=→E+→E−
=14πε0q(r−a)2ˆp−14πε0q(r−a)2ˆp⇒→Etot=14πε0(1(r−a)2−1(r−a)2)ˆp
→Etot=14πε0q(4ra(r2−a2)2)ˆp
Note that the total electric field is along →E+ since +q is closer to C than -q .
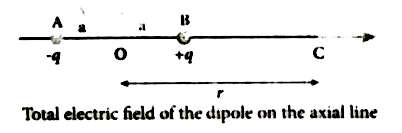
The direction of →Etot is shown in Figure If the point C is very far away from the dipole then (r>>a) . Under this limit the term (r2−a2)2zr4 . Substituting this into equation we get
→Etot=14πε0(4aqr3)ˆP(r>>a)
since 2 aq ˆp=→p
→Etot=14πε02→pr3 (r>>a)
If the point C is chosen on the left side of the dipole the total electric field is still in the direction of →p .
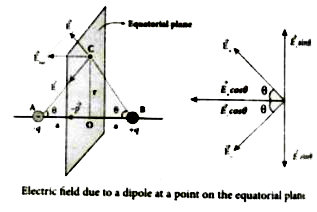
Case (ii) Electric field due to an electric dipole at a point on the equatorial plane
Consider a point C at a distance r from the midpoint O of the dipole on the equatorial plane as shown in Figure. Since the point C is equi -distant from +q and -q the magnitude of the electric fields of +q and -q are the same . The direction of →E+ is along BC and the direction of →E− is along CA. →E+ and →E− are resolved into two components one component parallel to the dipole axis and the other perpendicular to it . The perpendicular components ∣∣→E+∣∣sinθ and |→–––(−)|sinθ are oppositely directed and cancel each other . The magnitude of the total electric field at point C is the sum of the parallel components of →E+ and →E− and its direction is along −ˆP
→Etot=−∣∣→E+∣∣cosθˆp−∣∣→E−∣∣cosθˆp ⋯(1) ⋯(1)
The magnitudes →E+ and →E− are the same and are given by
∣∣→E+∣∣=∣∣→E−∣∣=14πε0q(r2+a2) ⋯(2)
By substituting equation (1) into equation (2) we get
→Etot=−14πε02qcosθ(r2+a2)ˆp=−14πε02qa(r2+a2)32ˆP since cos θq√r2+a2
At very large distances (r>>a) the equation becomes
→Etot=−14πε0Pr3(r>>a)
Topper's Solved these Questions
- ELECTROSTATICS Book:FULL MARKSChapter:ELECTROSTATICS Exercise:EXERCISES
Explore 15 Videos
- ELECTROSTATICS Book:FULL MARKSChapter:ELECTROSTATICS Exercise:ADDITIONAL QUESTIONS SOLVED ( Multiple choice questions : )
Explore 57 Videos
- ELECTROSTATICS Book:FULL MARKSChapter:ELECTROSTATICS Exercise:Textual Evaluation Solved (II. Short Answer Questions : )
Explore 21 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:FULL MARKSChapter:DUAL NATURE OF RADIATION AND MATTERExercise:ADDITIONAL QUESTIONS -( ADDITIONAL NUMERICAL PROBLEMS : )
Explore 10 Videos
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT Book:FULL MARKSChapter:MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT Exercise:ADDITIONAL QUESTIONS SOLVED - NUMERICAL PROBLEMS :
Explore 4 Videos
Similar Questions
The angle between the electric dipole moment and electric field due to the dipole on its axial and equatorial lines respectively are
View SolutionAssertion: The electric field due to dipole on its axis line at a distance r is E. Then electric field due to the same dipole on the equatorial line and at the same distance will be E2
Reason: Electric field due to dipole varies inversely as the square of distance.
View Solution
Knowledge Check
If Ea be the electric field strength of a short dipole at a point on its axial line and Ee that on the equatorial line at the same distance, then
AEa=4EqBEq=2EaCEa=2EqDEq=3EaAssertion: The electric field due to dipole on its axis line at a distance r is E. Then electric field due to the same dipole on the equatorial line and at the same distance will be E2
Reason: Electric field due to dipole varies inversely as the square of distance.Aif both Assertion and Reason are true and the Reason is correct explanation of the Assertion.BIf both Assertion and Reason are true but Reason is not the correct explanation of the Assertion.Cif Assertion is true, but the Reason is false.Dif both Assertion and Reason are falseIf Ea be the electric field of a short dipole at a point on its axial line and Ee that on the equatorial line at the same distance ,then
AEa=2EeBEe=2EaCEa=EeDnone of these
If Ea be the electric field strength of a short dipole at a point on its axial line and Ee that on the equatorial line at the same distance, then
View SolutionIf Ea be the electric field strength of a short dipole at a point on its axial line and Ee that on the equatorial line at the same distance, then
View SolutionWhat is the ratio of electric field intensity at a point on the equatorial line to the field at a point on axial line when the points are at the same distance from the centre of the dipole ?
View SolutionShow mathematically that the electric field due to a short dipole at a distance 'd' along its axis is twice the value of field at the same distance along the equatorial line.
View SolutionIf Ea be the electric field strength of a short dipole at a point on its axial line and Ee that on the equatorial line at the same distance, then
View Solution
