How do we determine the electric field due to a continuous charge distribution ? Explain. Electric field due to continous charge distribution Solution in Tamil

Video Solution

Text Solution

Verified by Experts

The electric charge is quantized microscopically। The expressions of Coulomb.s Law, superposition principle force and electric field are applicable to only point charges। While dealing with the electric field due to a charged sphere or a charged wire etc।, it is very difficult to look at individual charges in these charged bodies। Therefore, it is assumed that charge is distributed continuously on the charged bodies and the discrete nature of charges is not considered here। The electric field due to such continuous charge distributions is found by invoking the method of calculus।
Consider the following charged object of irregular shape।The entire charged object is divided into a large number of charge elements $△ q_{1}$ , $△ q_{2}$ , $△ q_{3}$ ................ $△ q_{n}$
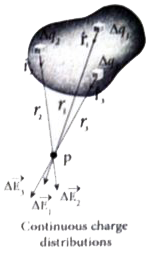and each charge element Aq is taken as a point charge
The electric field at a point P due to a charged object is approximately Here $△$ qi is the ith charge element, $i^{। t h}$ , is the distance of the point P from the i." charge clement and $ˆ r$ is the unit vector from ith charge element to the point P।
However the equation is only an approximation। To incorporate the continuous distribution of charge, we take the limit $△ q \to 0 (= d q) ।$ In this limit, the summation in the equation becomes an integration and takes the following form
$\to E = \frac{1}{4 π ε_{0}} \int \frac{d q}{r^{2}} ˆ r$

Here r is the distance of the point P from the infinitesimal charge dy and r is the unit vector from dq to point P। Even though the electric field for a continuous charge distribution is difficult to evaluate, the force experienced by some test charge q in this electric field is still given by $\to F = q \to E ।$
(a) Line charge distribution: If the charge Q is uniformly distributed along the wire of length L, then linear charge density (charge per unit length) is 2 = । Its unit is coulomb per meter $(C m^{- 1})$ । The charge present in the infinitesimal length dl is dq $= γ d l ।$
The electric field due to the line of total charge Q is given by
$\to E = \frac{1}{4 π ε_{0}} \int \frac{γ d l}{r^{2}} ˆ r = \frac{γ}{4 π ε_{0}} \int \frac{d l}{r^{2}} ˆ r$
(b) Surface charge distribution: If the charge Q is uniformly distributed on a surface area A, then surface charge density (charge per unit area) is $σ = \frac{Q}{A}$ । Its unit is coulomb per square meter $(C m^{- 2}$ ।
The charge present in the infinitesimal area dA is dq = $σ d A$ । The electric field due to a of total charge Q is given by
$\to E = \frac{1}{4 π ε_{0}} \int \frac{α d a}{r^{2}} ˆ r = \frac{1}{4 π ε_{0}} α \int \frac{d a}{r^{2}} ˆ r$
(c) Volume charge distribution: If the charge Q is uniformly distributed in a volume V, then volume charge density (charge per unit volume) is given by p= Q/V। Its unit is coulomb per cubic meter $(C m^{- 3})$ The charge present in the infinitesimal volume element dVN is dq = pdV।
The electric field due to a volume of total charge Q is given by
$\to E = \frac{1}{4 π ε_{0}} \int \frac{ρ d V}{r^{2}} = \frac{1}{4 π ε_{0}} ρ \int \frac{d V}{r^{2}} ˆ r$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

FULL MARKS-SAMPLE PAPER 9-PART-IV

Home
Ask Doubt
Profile