Find the electric field intensity due to continuous charge distribution.
Electric field intensity due to linear charge distribution.
Consider a line PQ having length l and charge q. Let Δl be the small line element having charge ΔQ. Then linear charge density γ of a wire is
λ=ΔQΔl⇒ΔQ=λΔl.
Now the electric field due to charge element λΔ is given by
Δ→E=14πɛ0λΔlr.2
Where r. is the distance between the charge element and point P. Then the total electric field due to the linear charge distribution is
→E=14πɛ0∑ullΔlλΔlr.2ˆr.
Similarly, the total electric field intensity due to the surface charge density is 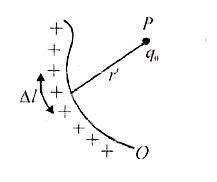
→E=14πɛ0∑ullΔsσΔSr.2ˆr.
Where σ is the surface charge density.
i.e σ=ΔQΔV
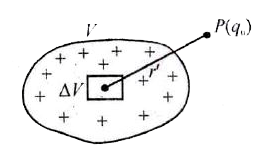
Similarly, total electric field intensity due to volume charge distribution is
→E=14πɛ0∑ullΔsρΔSr.2ˆr.
Where ρ is the volume charge density.
i.e. ρ=ΔQΔV 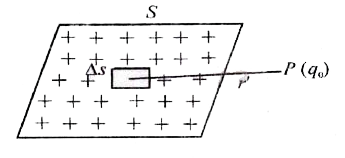
Similar Questions
Statement 1:Electric field intensity at surface of uniformly charged spehrical shell is E if the shell is puncurted at a point then intensity at punctured point becomed E/2.
Statement 2:Electric field intensity due to spherical charge distribution can be found out by using GaussLaw.
View SolutionPotential due to continuous charge distribution and self energy
View Solution
Knowledge Check
Assertion: Electric field intensity at a point due to a positive charge is always opposite in direction to electric field intensity due to negative charge, and it is independent to locațions of charges.
Reason: The direction of electric field due to a point charge is away from the positive charge and towards the negative charge along the line joining the point charge and location where the electric field is to be calculated.AIf both assertion and reason are correct and reason is a correct explanation of the assertion .BIf both assertion and reason are correct but reason is not the correct explanation of assertionCIf assertion is correct but reason is incorrectDIf assertion is incorrect but reason is correct.Electric field intensity at point P due to charge distributed over a sphere is:
 AE=14πε0qrBE=σR2ε0r2CE=14πε0qrDE=0
AE=14πε0qrBE=σR2ε0r2CE=14πε0qrDE=0
Find expression for electric field intensity due to a uniformly charged thin spherical shell at a point outside the shell.
View SolutionApply Gauss's theorem to find an expression for the electric field intensity at a point due to a point charge.
View SolutionDerive an expression for electric field intensity at a point due to point charge.
View SolutionDerive an expression for electric field intensity at a point due to point charge.
View SolutionFind the direction of electric field at P for the charge distribution as shown infigure.
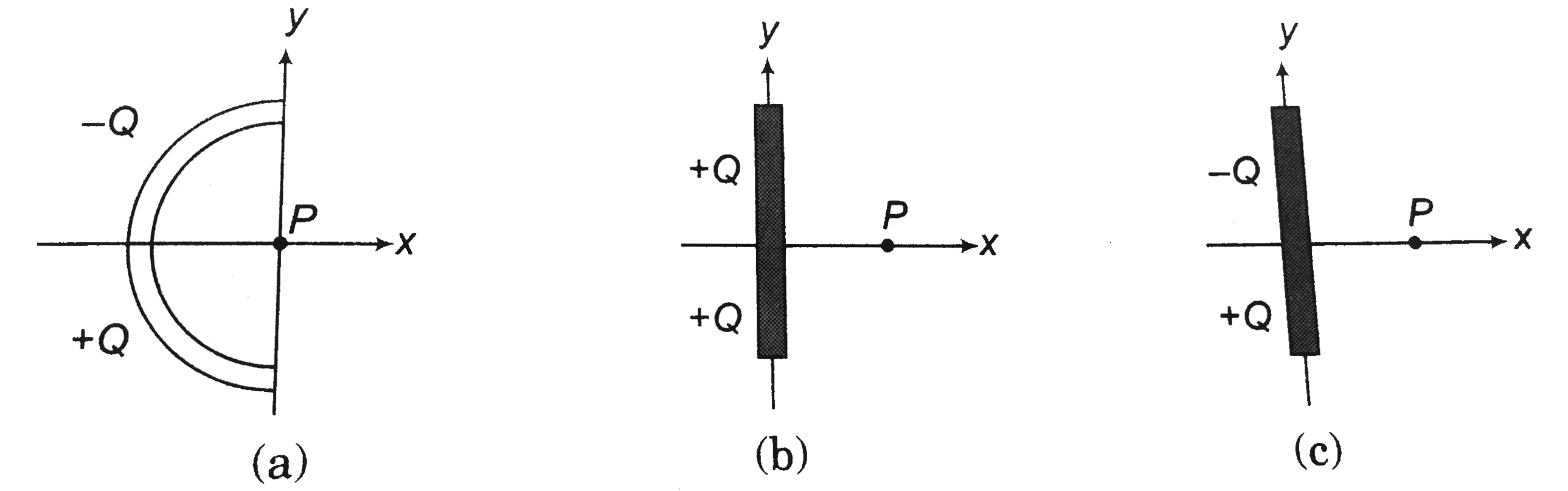
View SolutionFind the direction of electric field at P for the charge distribution as shown infigure.

View Solution
