Two particles are projected simultaneously from a point with different speeds and along the different directions. When both the particles are in air, then
what will be the path of one particle with respect to the other ?
parabola
hyperbola
straight line
ellipse
The correct Answer is:C
To solve the problem of determining the path of one particle with respect to the other when two particles are projected simultaneously from a point with different speeds and directions, we can follow these steps:
1. Understanding the Problem:
- We have two particles, A and B, projected from the same point.
- Each particle has a different speed and is projected at different angles.
2. Define the Velocities:
- Let the velocity of particle A be →ua and the velocity of particle B be →ub.
- The components of the velocities can be defined as:
- For particle A:
- Horizontal component: uacos(θa)
- Vertical component: uasin(θa)
- For particle B:
- Horizontal component: ubcos(θb)
- Vertical component: ubsin(θb)
3. Define the Accelerations:
- Both particles experience gravitational acceleration downwards, which can be represented as:
- →g=−g^j
4. Relative Motion:
- To find the path of one particle with respect to the other, we need to analyze their relative motion.
- The relative velocity of particle A with respect to particle B is given by:
→vAB=→ua−→ub
- The relative acceleration of particle A with respect to particle B is:
→aAB=→aa−→ab=0
- Since both particles have the same acceleration due to gravity, their relative acceleration is zero.
5. Conclusion on Path:
- Since the relative acceleration is zero, the relative velocity →vAB remains constant.
- This means that particle A will appear to move in a straight line with respect to particle B, as there is no change in the relative velocity.
6. Final Answer:
- The path of one particle with respect to the other will be a straight line.
- We have two particles, A and B, projected from the same point.
- Each particle has a different speed and is projected at different angles.
- Let the velocity of particle A be →ua and the velocity of particle B be →ub.
- The components of the velocities can be defined as:
- For particle A:
- Horizontal component: uacos(θa)
- Vertical component: uasin(θa)
- For particle B:
- Horizontal component: ubcos(θb)
- Vertical component: ubsin(θb)
- Both particles experience gravitational acceleration downwards, which can be represented as:
- →g=−g^j
- To find the path of one particle with respect to the other, we need to analyze their relative motion.
- The relative velocity of particle A with respect to particle B is given by:
→vAB=→ua−→ub
- The relative acceleration of particle A with respect to particle B is:
→aAB=→aa−→ab=0
- Since both particles have the same acceleration due to gravity, their relative acceleration is zero.
- Since the relative acceleration is zero, the relative velocity →vAB remains constant.
- This means that particle A will appear to move in a straight line with respect to particle B, as there is no change in the relative velocity.
- The path of one particle with respect to the other will be a straight line.
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - COMPETITION FILE OBJECTIVE TYPE QUESTIONS (B. Multiple Choice Questions)
38 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - COMPETITION FILE OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other Boards for Engineering Entrance)
14 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Revision Exercises (Numerical Problems)
26 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
Two particles 1 and 2 start simultaneously from origin and move along the positive X direction. Initial velocity of both particles is zero. The acceleration of the two particles depends on their displacement (x) as shown in fig.
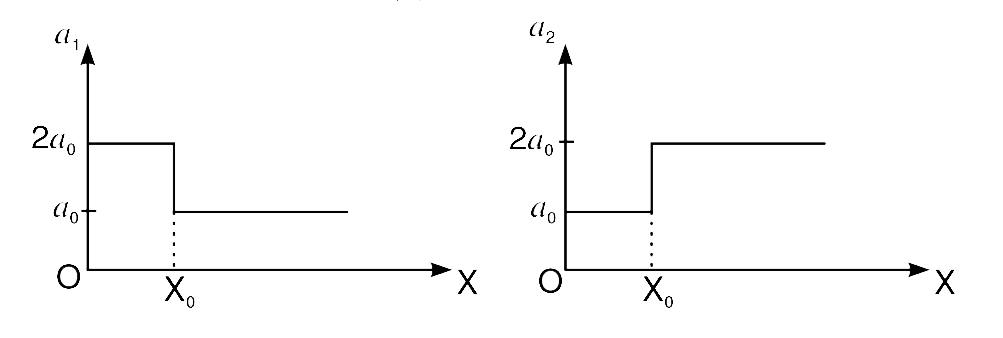
(a) Particles 1 and 2 take t1 and t2 time respectively for their displacement to become x0. Find t2t1.
(b) Which particle will cover 2x0 distance in least time? Which particle will cross the point x=2x0 with greater speed?
(c) The two particles have same speed at a certain time after the start. Calculate this common speed in terms of a0 and x0.
View SolutionTwo particles start from the same point with different speeds but one moves along y=asinωx and other moves along curve y=cosωx
View Solution
Knowledge Check
Two particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then :
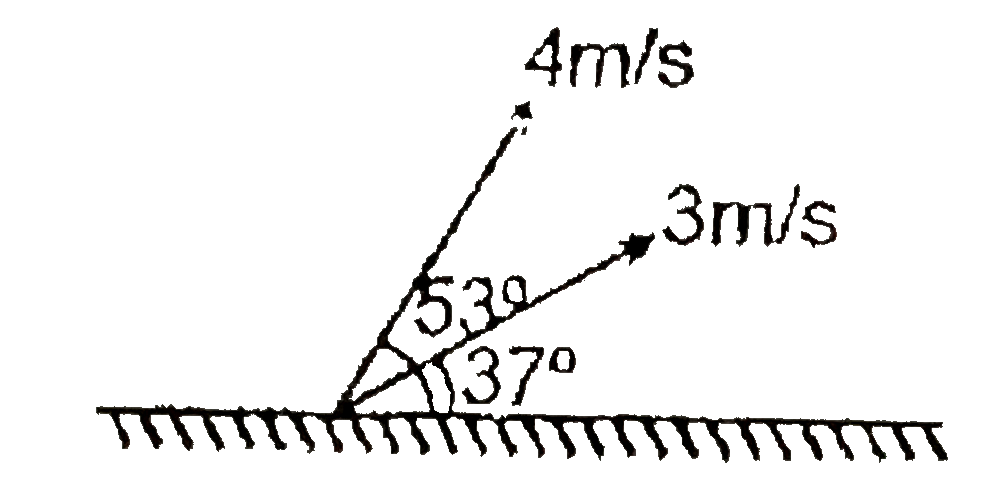 ATheir relative velocity is along horizontal direction.BTheir relative acceleration is non-zero and it is along vertical direction.CThey will hit the surface simultaneously.DTheir relative velocity is constant and has magnitude 1.4m/s
ATheir relative velocity is along horizontal direction.BTheir relative acceleration is non-zero and it is along vertical direction.CThey will hit the surface simultaneously.DTheir relative velocity is constant and has magnitude 1.4m/sTwo particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then:
 ATheir relative velocity is along vertical directionBTheir relative acceleration is non-zero and it is along vertical directionCThey will hit the surface simultaneouslyDTheir relative velocity is constant and has magnitude 1.4m/s
ATheir relative velocity is along vertical directionBTheir relative acceleration is non-zero and it is along vertical directionCThey will hit the surface simultaneouslyDTheir relative velocity is constant and has magnitude 1.4m/sA number of particles are projected from a given point with equal velocities in different directions in the same vertical plane. At any instant they will lie on
AparabolaBcircleChyperbolaDrectangle
Two particles are projected simultaneously from the same point, with the same speed, in the same vertical plane, and at different angles with the horizontal in a uniform gravitational field acting vertically downwards. A frame of reference is fixed to one particle. The position vector of the other particle , as observed from this frame, is →r. Which of the following statement is correct?
View SolutionStatement-1: Two stones were projected simultaneously from same point with same speed at different angles from horizontal as shown. They may collide at the point of intersection of their paths.
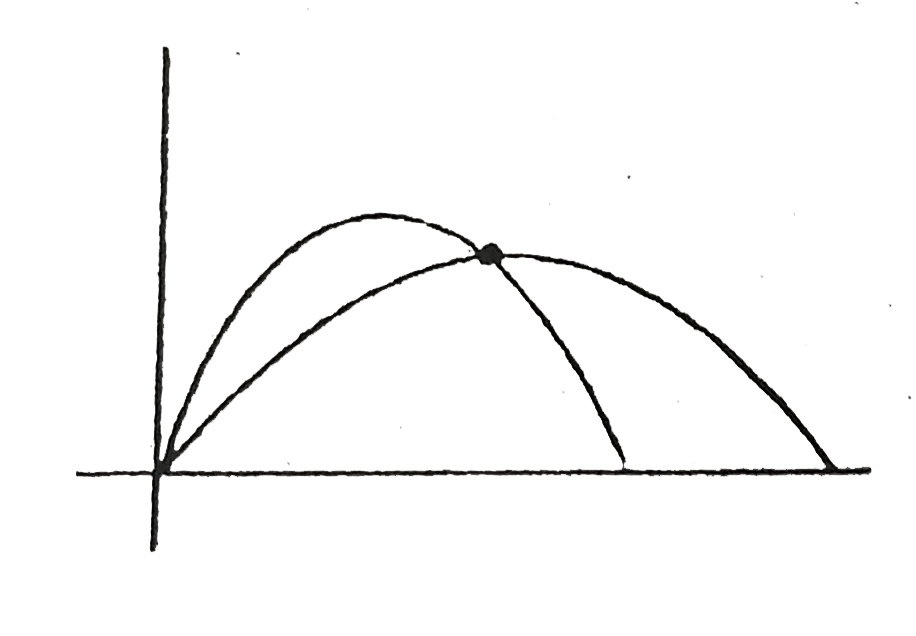
Statement-2: For two particles to collide they must be at the same point in space simultaneously.
View SolutionTwo particles are projected from the same point, with the same speed, in the same vertical plane, at different angles with the horizontal.A frame of references is fixed to one particle.The position vector of the other particle as observed from this frame is →rWhich of the following statements are corrects?
View SolutionTwo particles A and B are projected simultaneously from a fixed point of the ground. Particle A is projected on a smooth horizontal surface with speed v, while particle B is projected in air with speed v, while particle B is projected in air with speed 2v√3. If particle B hits the particle A, the angle of projection of B with the vertical is
View SolutionTwo particles A and B are projected from the same point in different direction in such a manner that their velocity vectors are shown in the diagram :−
 .
.
View Solution
