Two particles A and B are projected simultaneously in horizontal direction with speed 50m/s and 100m/s respectively . If tAandtB are the time taken by the projectiles to hit the ground by the particles A and B respectively, then
tA=tB
ta>tB
tA<tB
Information is insufficient to compare tAandtB.
The correct Answer is:A
To solve the problem, we need to analyze the motion of both particles A and B. Since both particles are projected horizontally, the time taken for each particle to hit the ground depends solely on the vertical motion, which is influenced by gravity.
1. Understanding the Vertical Motion:
- Both particles A and B are projected horizontally. The only force acting on them in the vertical direction is gravity (g = 9.81 m/s²).
- The initial vertical velocity (u_y) for both particles is 0 m/s since they are projected horizontally.
2. Using the Equation of Motion:
- The time taken to hit the ground can be derived from the second equation of motion:
s=uyt+12gt2
- Here, s is the vertical distance fallen (which is the same for both particles when they hit the ground), uy is the initial vertical velocity (0 m/s), g is the acceleration due to gravity, and t is the time taken to hit the ground.
3. Simplifying the Equation:
- Since uy=0, the equation simplifies to:
s=12gt2
- Rearranging gives:
t2=2sg
- Thus, the time t can be expressed as:
t=√2sg
4. Conclusion About Time Taken:
- Since both particles A and B fall the same vertical distance s and experience the same acceleration due to gravity g, the time taken tA for particle A and tB for particle B to hit the ground will be the same:
tA=tB
Final Answer:
The time taken by both particles A and B to hit the ground is the same:
tA=tB
- Both particles A and B are projected horizontally. The only force acting on them in the vertical direction is gravity (g = 9.81 m/s²).
- The initial vertical velocity (u_y) for both particles is 0 m/s since they are projected horizontally.
- The time taken to hit the ground can be derived from the second equation of motion:
s=uyt+12gt2
- Here, s is the vertical distance fallen (which is the same for both particles when they hit the ground), uy is the initial vertical velocity (0 m/s), g is the acceleration due to gravity, and t is the time taken to hit the ground.
- Since uy=0, the equation simplifies to:
s=12gt2
- Rearranging gives:
t2=2sg
- Thus, the time t can be expressed as:
t=√2sg
- Since both particles A and B fall the same vertical distance s and experience the same acceleration due to gravity g, the time taken tA for particle A and tB for particle B to hit the ground will be the same:
tA=tB
The time taken by both particles A and B to hit the ground is the same:
tA=tB
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - COMPETITION FILE OBJECTIVE TYPE QUESTIONS (B. Multiple Choice Questions)38videos
MOTION IN A PLANE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - COMPETITION FILE OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other Boards for Engineering Entrance)14videos
MOTION IN A PLANE
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Revision Exercises (Numerical Problems)26videos
MOTION IN A PLANE
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test16videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST16videos
MOTION IN A STRAIGHT LINE
Similar Questions
Two particles A and B are projected simultaneously in the directins shown in figure with velocities vA=20m/sandvB=10m/s respectively. They collide in air after 12 s. Find
(a) the angle θ
(b) the distance x.
 . View Solution
. View SolutionTwo particles A and B of equal mass are projected simultaneously with speed 10 m/s each as shown in figure. Find the co-ordinate of COM at t=10 s
View Solution
Knowledge Check
- Question 1 - Select One
Two particles A and B are projected simultaneously in the direction shown in the figure with velocities VA=20m/s and VB=10m/s respectively. If they collide in air after 1/2 sec. then
 Athe angle θ is 60∘Bthe distance x is 5√3mCthe angle θ is 30∘DThe distance x is 15√3m
Athe angle θ is 60∘Bthe distance x is 5√3mCthe angle θ is 30∘DThe distance x is 15√3m - Question 2 - Select One
Two projectiles are projected simultaneously from two towers as shwon in figure. If the projectiles collide in the air, then find the distance "s" between the towers.
 A10mB20mC30mD40m
A10mB20mC30mD40m - Question 3 - Select One
Two particles A and B are projected simultaneously from a fixed point of the ground. Particle A is projected on a smooth horizontal surface with speed v, while particle B is projected in air with speed v, while particle B is projected in air with speed 2v√3. If particle B hits the particle A, the angle of projection of B with the vertical is
A30∘B60∘CBoth (a) and (b)D45∘
Two particles A and B start at O travel in opposite directions along the circular path at constant speed vA=0.7m/s and vB=1.5m/s respectively. Determine the time when they collide and the magnitude of the acceleration of B just before this happening. (radius=5m)
 View Solution
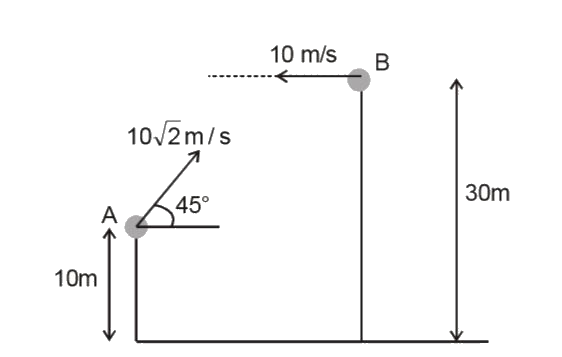
View SolutionTwo particles A and B are projected simultaneously from two towers of heights 10 m and 20m respectively. Particle A is projected with an initial speed of 10√2m/s at an angle of 45∘ with horizontal, while particle B is projected horizontally with speed 10m/s. If they collide in air, what is the distance d between the towers?
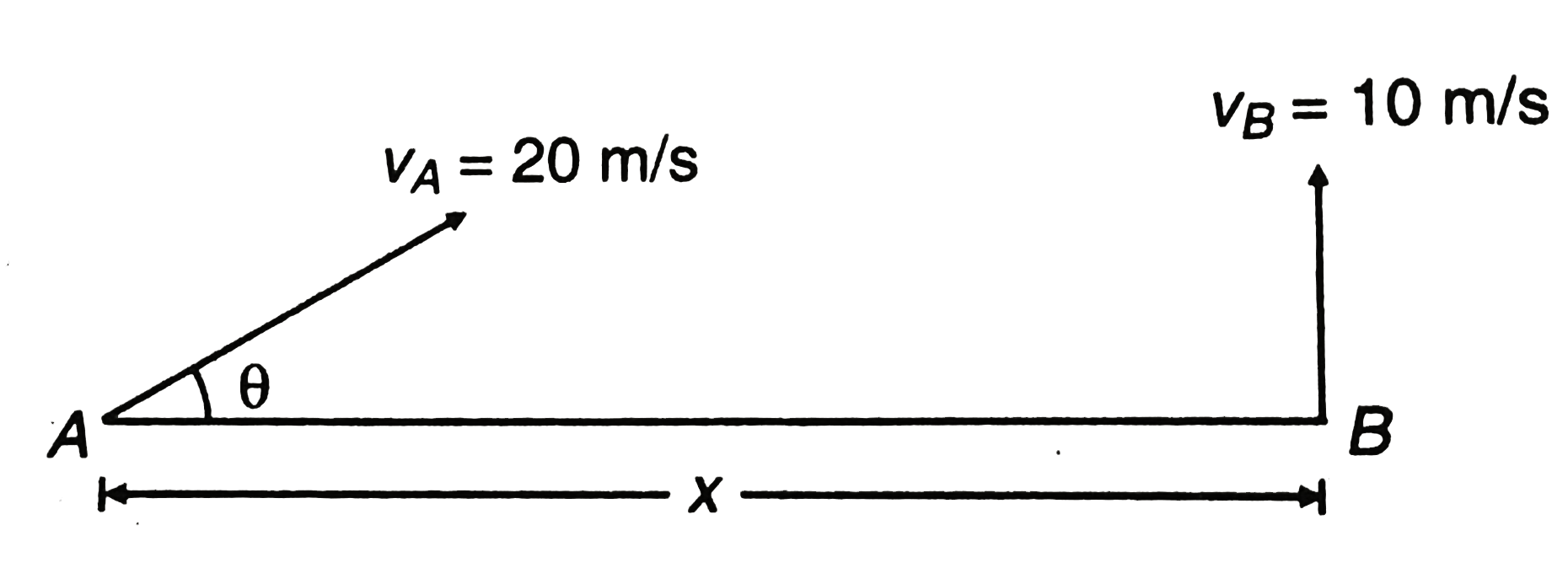 View Solution
View SolutionTwo particles are simultaneously thrown in horizontal direction from two points on a riverbank, which are at certain height above the water surface. The initial velocities of the particles are v1=5m/sandv2=7.5m/s respectively. Both particles fall into the water at the same time. First particles enters the water at a point s = 10 m from the bank. Determine
(a) the time of flight of the two particles,
(b) the height from which they are thrown,
(c) the point where the second particle falls in water.View SolutionTwo particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
View SolutionTwo particles P and Q simultaneously start moving from point A with velocities 15m/s and 20m/s respectively. The two particles move with acceleration equal in magnitude but opposite in direction. When P overtakes Q and B then its velocity is 30m/s the velocity of Q at point B will be
View Solution

