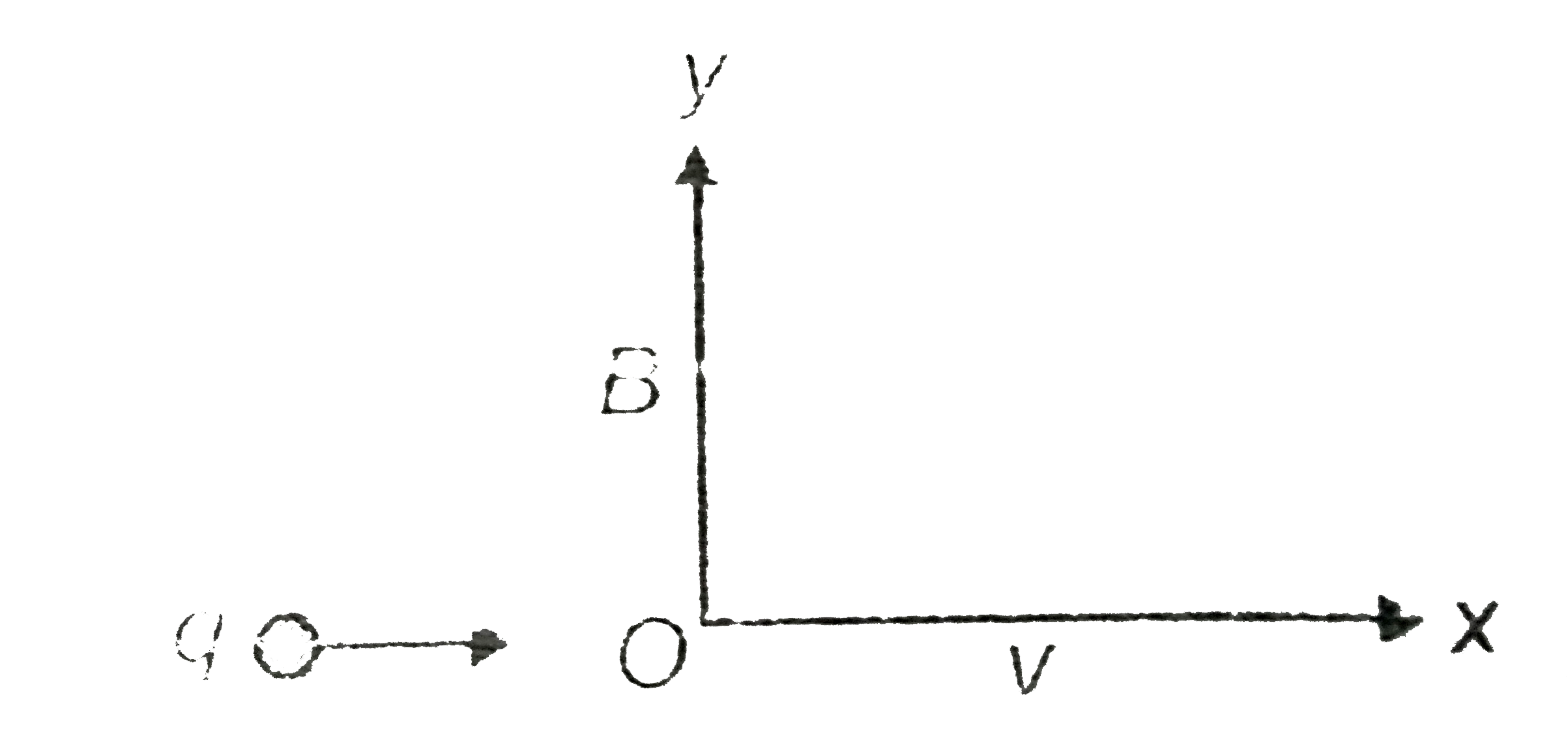
A positively charged particle is moving towards the east direction and is found to get deviated towards south. What is the possible direction of the magnetic field?
West
Upward
Downward
North
The correct Answer is:b
To determine the direction of the magnetic field when a positively charged particle is moving towards the east and deviates towards the south, we can use the right-hand rule and the relationship between force, velocity, and magnetic field.
1. Identify the Given Information:
- The particle is positively charged.
- The particle is moving towards the east (let's denote this direction as the positive x-direction).
- The particle is deviating towards the south (let's denote this direction as the negative y-direction).
2. Define the Directions:
- Let the east direction be represented by the unit vector ^i (positive x-direction).
- Let the south direction be represented by the unit vector −^j (negative y-direction).
- The magnetic field direction is what we need to find.
3. Use the Lorentz Force Equation:
The force F on a charged particle moving in a magnetic field is given by:
F=q(v×B)
where:
- q is the charge of the particle,
- v is the velocity vector,
- B is the magnetic field vector.
4. Set Up the Vectors:
- The velocity vector v can be represented as:
v=v^i
- The force vector F is directed south, which can be represented as:
F=−F^j
5. Apply the Right-Hand Rule:
- According to the right-hand rule, to find the direction of the magnetic field B, we can rearrange the equation:
F=q(v×B)
- Since q is positive, the direction of F is the same as v×B.
6. Cross Product Analysis:
- We know that:
F=−F^jandv=v^i
- Therefore, we need to find B such that:
^i×B=−^j
- The cross product ^i×^j=^k (out of the plane), and to get −^j, we need B to be in the positive ^k direction.
7. Conclusion:
- The direction of the magnetic field B must be upwards, which can be represented as ^k (positive z-direction).
Final Answer:
The possible direction of the magnetic field is upwards.
- The particle is positively charged.
- The particle is moving towards the east (let's denote this direction as the positive x-direction).
- The particle is deviating towards the south (let's denote this direction as the negative y-direction).
- Let the east direction be represented by the unit vector ^i (positive x-direction).
- Let the south direction be represented by the unit vector −^j (negative y-direction).
- The magnetic field direction is what we need to find.
The force F on a charged particle moving in a magnetic field is given by:
F=q(v×B)
where:
- q is the charge of the particle,
- v is the velocity vector,
- B is the magnetic field vector.
- The velocity vector v can be represented as:
v=v^i
- The force vector F is directed south, which can be represented as:
F=−F^j
- According to the right-hand rule, to find the direction of the magnetic field B, we can rearrange the equation:
F=q(v×B)
- Since q is positive, the direction of F is the same as v×B.
- We know that:
F=−F^jandv=v^i
- Therefore, we need to find B such that:
^i×B=−^j
- The cross product ^i×^j=^k (out of the plane), and to get −^j, we need B to be in the positive ^k direction.
- The direction of the magnetic field B must be upwards, which can be represented as ^k (positive z-direction).
The possible direction of the magnetic field is upwards.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)
Explore 79 Videos
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)
Explore 28 Videos
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:Revision Exercises (Numerical Problems )
Explore 18 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
- NUCLEIBook:MODERN PUBLICATIONChapter:NUCLEIExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 15 Videos
Similar Questions
Knowledge Check
A positive charge is moving towards an observer. The direction of magnetic induction lines is
AclockwiseBanticlockwiseCrightDleftA positively charged particle (alpha particle) projected towards west is deflected towards north by a magnetic field. The direction of magnetic field is ............
Atowards southBtowards eastCdownwardDupwardA particle is moving towards east enters in a magnetic field directed towards north and deflected in vertically downward direction. The charged particle is
Aan electronBa protonCan alpha particleDa neutron
A particle initially moving towards south in a vertically downward magnetic field is deflected toward the east. What is the sign of the charge on the particle?
View SolutionIf a positively charged particle is moving as shown in the figure, then it will be deflected due to magnetic field towards-

View SolutionA positively charged particle (alpha-particle) projected towards west is deflected towards north be a magnetic field. The direction of magnetic field is:
View SolutionA positively charged particle (alpha-particle) projected towards west is deflected towards north be a magnetic field. The direction of magnetic field is:
View SolutionA positively charged particle projected towards east is deflected towards north by a magnetic field. The field may be
View Solution