In the XY-plane, the regiony y>0 has a uniform magnetic field B1ˆk and the region y<0 has another uniform magnetic field B2ˆk . A positively charged particle is projected from the origin along the positive Y-axis with speed v0=πms−1 at t=0 , as shown in the figure. Neglect gravity in this problem. Let t=T be the time when the particle croasca the X axia from below for the first time If B2=4B1, the average velocity of the particle, in ms−1 , along the X - axis in the time interval T is ________ .

The correct Answer is:2.00
In time interval T, particle covers half circle in field B, and other half circle in fieldB1 and other half circle in field B2.
R1=mv0qB1,R2=mv0qB2=mv04qB1( given B2=4B1)
Distance along X - axis Δx=2(R1+R2)=5mv02qB1=5mπ2qB1
Total time T=πmqB1+πmqB2=πmqB1+πm4qB1=5πm4qB1
Magnitude of average speed =ΔxT=2qB15πm4qB1=2m/s
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - CHAPTER PRACTICE TEST
13 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (MATRIX MATCH TYPE QUESTIONS)
1 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
In the XY- plane , the region y>0 has a uniform magnetic field B1ˆk and the region y<0has another uniform magnetic field B2ˆk. A positively charged particle is projected from the origin along the positive y- axis with speed v0=πms−1 at t=0 , as shown in the figure . Neglect gravity in this problem . Let t=T be the time when the particle crosses the X- axis from below for the first time . If B2=4B1, the average speed to the particle , in ms−1, along the x- axis in the time interval T is __________ .
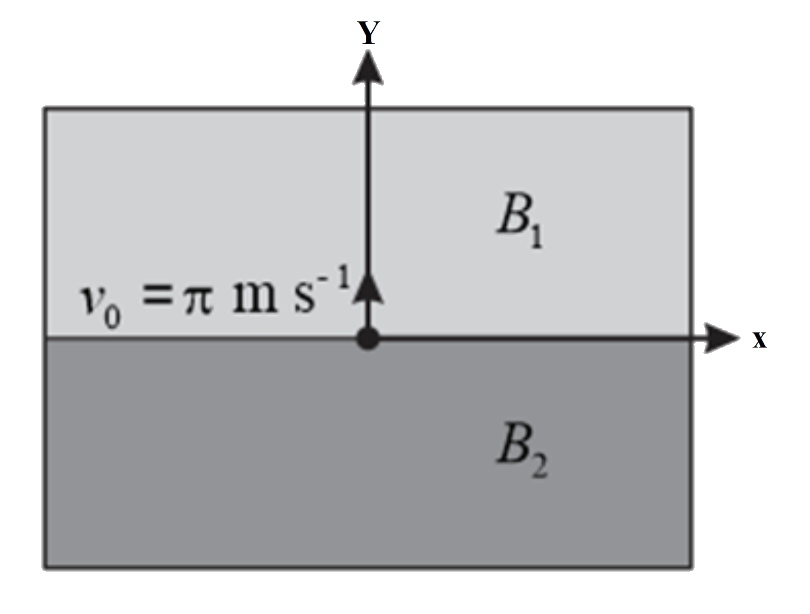
View SolutionIn the XY- plane , the region y>0 has a uniform magnetic field B1ˆk and the region y<0has another uniform magnetic field B2ˆk. A positively charged particle is projected from the origin along the positive y- axis with speed v0=πms−1 at t=0 , as shown in the figure . Neglect gravity in this problem . Let t=T be the time when the particle crosses the X- axis from below for the first time . If B2=4B1, the average speed to the particle , in ms−1, along the x- axis in the time interval T is __________ .

View Solution
Knowledge Check
A uniform electric field →E in the y-direction and uniform magnetic field →B in the x-direction exists in free space. A particle of mass m and carrying charge g is projected from the origin with speed v0 along the y axis. The speed of the particle as a function of its y coordinate will be
A√v20+2qEymB√v20+qEymC√v20+4qEymDv0In region x>0 a uniform and constant magnetic field →B1=2B0ˆk exists. Another uniform and constant magnetic field →B2=B0ˆk exists in region x<0 A positively charged particle of mass m and charge q is crossing origin at time t =0 with a velocity ¯u=u0ˆi. The particle comes back to its initial position after a time : (B0,u0 are positive constants)
A32πmqB0B2πmqB0C3πmqB0DParticle does not come back to its initial positionA particle of mass m and having a positive charge q is projected from origin with speed v0 along the positive X-axis in a magnetic field B = −B0ˆK, where B0 is a positive constant. If the particle passes through (0,y,0), then y is equal to
A−2mv0qB0Bmv0qBC−mv0qBD2mv0qB0
In region x>0 a uniform and constant magnetic field →B1=2B0ˆk exists. Another uniform and constant magnetic field →B2=B0ˆk exists in region x<0 A positively charged particle of mass m and charge q is crossing origin at time t =0 with a velocity ¯u=u0ˆi. The particle comes back to its initial position after a time : (B0,u0 are positive constants)
View SolutionA particle of mass m and having a positive charge q is projected from origin with speed v0 along the positive X-axis in a magnetic field B = −B0ˆK, where B0 is a positive constant. If the particle passes through (0,y,0), then y is equal to
View SolutionA uniform magnetic field exists perpendicular to the plane of the figure and a uniform electric field exists in the plane of the figure in positive y direction. A charged particle, when projected along xy plane moves along the path shown in the figure. Is the particle positively charged or negatively charged?

View SolutionA particle of specific charge q/m=(π)C/kg is projected from the origin towards positive x-axis with a velocity of 10m/s in a uniform magnetic field →B=−2ˆK Tesla. The velocity →V of the particle after time t=1/6 s will be
View SolutionA particle of specific charge q/m=(π)C/kg is projected from the origin towards positive x-axis with a velocity of 10m/s in a uniform magnetic field →B=−2ˆK Tesla. The velocity →V of the particle after time t=1/6 s will be
View Solution
