In region x>0 a uniform and constant magnetic field →B1=2B0ˆk exists. Another uniform and constant magnetic field →B2=B0ˆk exists in region x<0 A positively charged particle of mass m and charge q is crossing origin at time t =0 with a velocity ¯u=u0ˆi. The particle comes back to its initial position after a time : (B0,u0 are positive constants)
a. 32πmqB0
b. 2πmqB0
c. 3πmqB0
d. Particle does not come back to its initial position
The correct Answer is:B
To solve the problem, we need to analyze the motion of a positively charged particle in two different magnetic fields. The particle crosses the origin at time t=0 with an initial velocity →u=u0^i.
1. Identify the Magnetic Fields:
- For x>0: The magnetic field is →B1=2B0^k.
- For x<0: The magnetic field is →B2=B0^k.
2. Determine the Force on the Particle:
- The magnetic force on a charged particle is given by →F=q→u×→B.
- At t=0, the particle has a velocity →u=u0^i.
- In the region x>0 (where →B1 is present):
→F1=q(u0^i)×(2B0^k)=2qB0u0^j
- This force acts in the positive y-direction, causing the particle to move in a circular path.
3. Calculate the Radius of the Circular Motion in x>0:
- The radius r1 of the circular path can be found using the formula:
r1=mvqB
- Here, v=u0 and B=2B0:
r1=mu0q(2B0)
4. Determine the Time Taken to Traverse the Circular Path in x>0:
- The time t1 to complete a half-circle (from x=0 to the maximum y position) is:
t1=πr1u0=π(mu0q(2B0))u0=πm2qB0
5. Analyze the Motion in x<0:
- In the region x<0, the magnetic field is →B2=B0^k.
- The radius r2 in this region is:
r2=mu0qB0
6. Calculate the Time Taken to Traverse the Circular Path in x<0:
- The time t2 to complete a half-circle in this region is:
t2=πr2u0=π(mu0qB0)u0=πmqB0
7. Total Time for the Particle to Return to the Initial Position:
- The total time T for the particle to return to its initial position is the sum of the times taken in both regions:
T=t1+t2+t1=πm2qB0+πmqB0+πm2qB0
- Simplifying this gives:
T=2πmqB0
Final Answer:
The total time taken for the particle to return to its initial position is:
T=2πmqB0
- For x>0: The magnetic field is →B1=2B0^k.
- For x<0: The magnetic field is →B2=B0^k.
- The magnetic force on a charged particle is given by →F=q→u×→B.
- At t=0, the particle has a velocity →u=u0^i.
- In the region x>0 (where →B1 is present):
→F1=q(u0^i)×(2B0^k)=2qB0u0^j
- This force acts in the positive y-direction, causing the particle to move in a circular path.
- The radius r1 of the circular path can be found using the formula:
r1=mvqB
- Here, v=u0 and B=2B0:
r1=mu0q(2B0)
- The time t1 to complete a half-circle (from x=0 to the maximum y position) is:
t1=πr1u0=π(mu0q(2B0))u0=πm2qB0
- In the region x<0, the magnetic field is →B2=B0^k.
- The radius r2 in this region is:
r2=mu0qB0
- The time t2 to complete a half-circle in this region is:
t2=πr2u0=π(mu0qB0)u0=πmqB0
- The total time T for the particle to return to its initial position is the sum of the times taken in both regions:
T=t1+t2+t1=πm2qB0+πmqB0+πm2qB0
- Simplifying this gives:
T=2πmqB0
The total time taken for the particle to return to its initial position is:
T=2πmqB0
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.489videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4920videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4611videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
A portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton
View SolutionA magnetic field →B=B0ˆj , exists in the region a<x<2a , and →B=−B0ˆj , in the region 2a<x<3a, where B0 is a positive constant . A positive point charge moving with a velocity →v=v0ˆi , where v0 is a positive constant , enters the magnetic field at x=a . The trajectory of the charge in this region can be like
 View Solution
View SolutionA uniform magnetic field →B=B0ˆk exists in a region. A current carrying wire is placed in x-y plane as show. Find the force acting on the wire AB, if each section of the wire is of length 'a'.
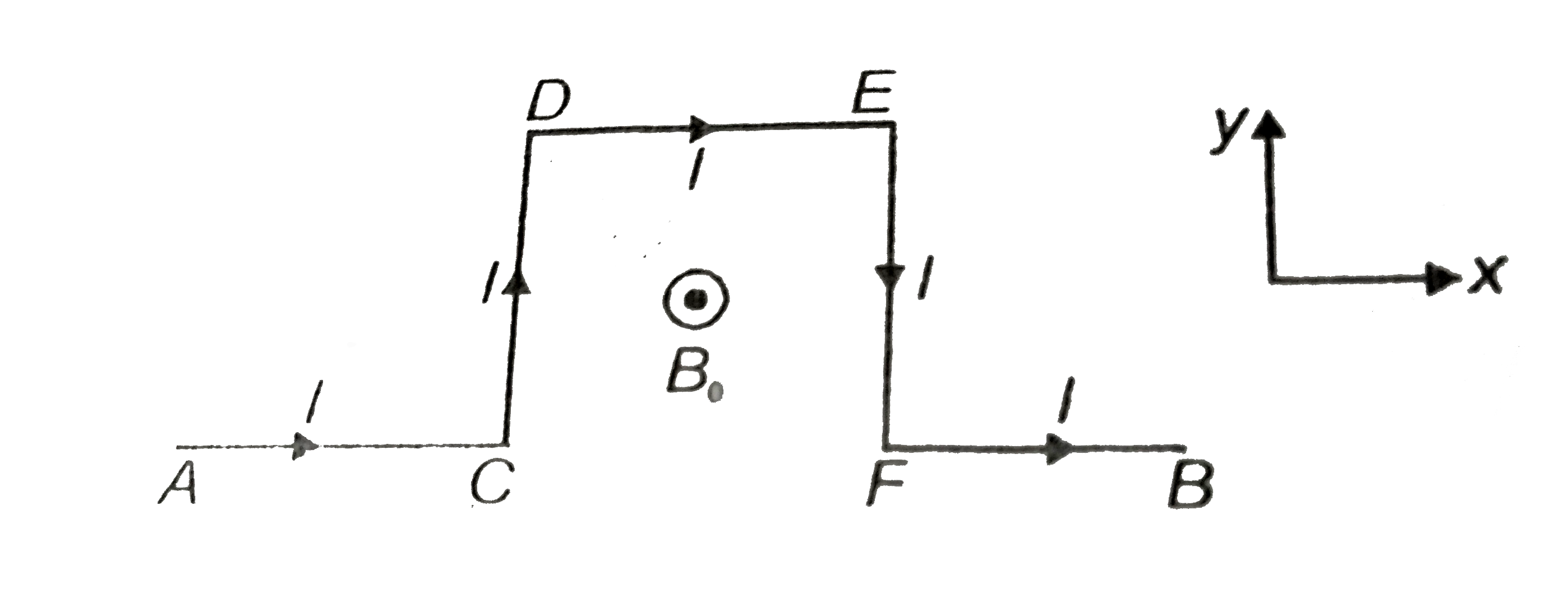 View Solution
View SolutionA rectangular loop of dimensions (a×b) carries a current i. A uniform magnetic field →B=B0ˆi exists in space. Then :
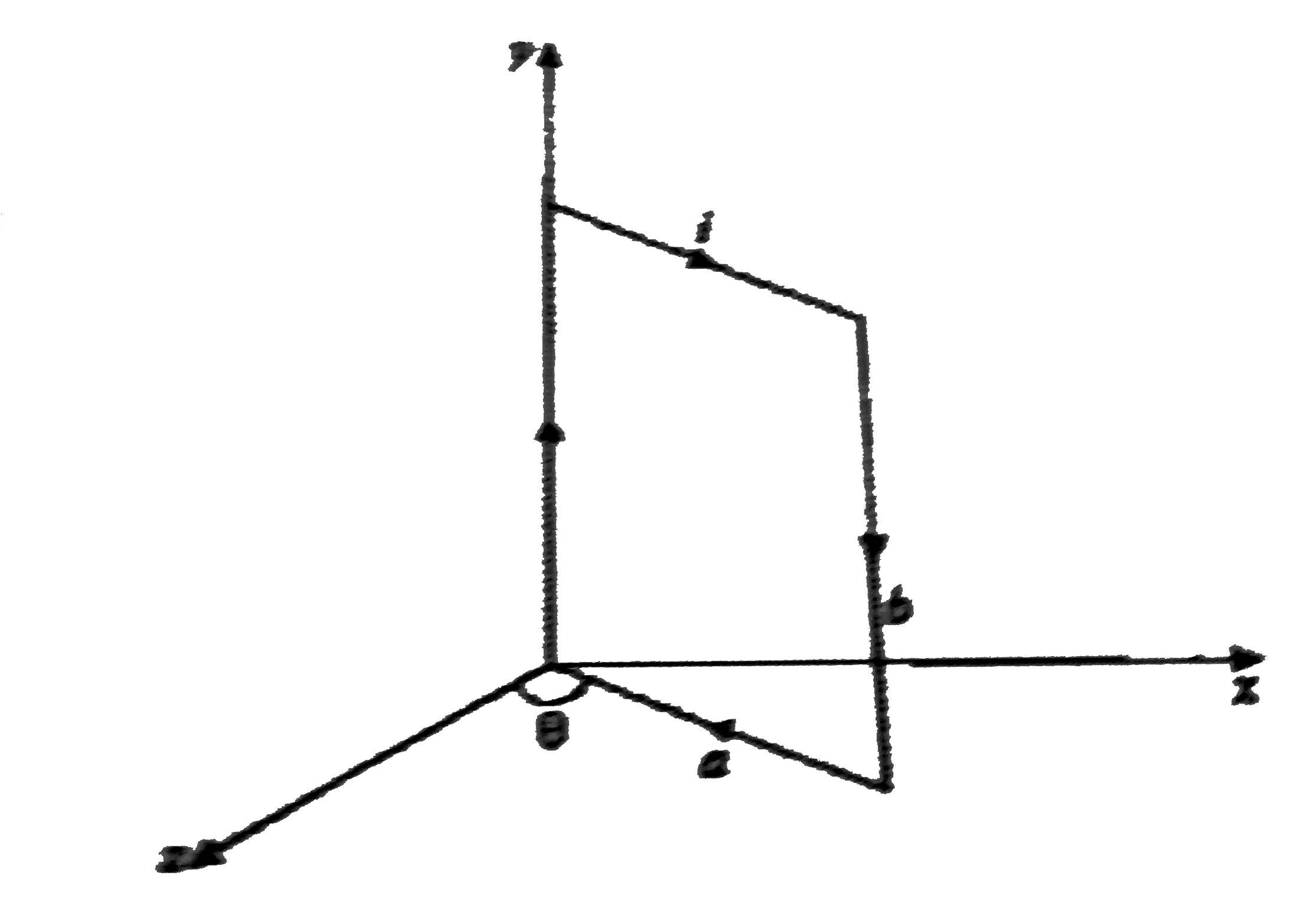 View Solution
View SolutionA circular loop of radius R carrying current I is kept in XZ plane. A uniform and constant magnetic field →B=(B0ˆi+2B0ˆj+3B0ˆk) exists in the region (B0− a positive constant). Then the magnitude of the torque acting on the loop will be
View SolutionA conductor AB of length l moves in xy plane with velocity →v=v0(ˆi−ˆj). A magnetic field →B=B0(ˆi+ˆj) exists in the region. The induced emf is
View SolutionIn a region at a distance r from z-axis, magnetic field →B=B0rtˆk is present where B0 is constant and t is time. Then the magnetic of induced electric field at a distance r from z-axis is given by
View SolutionIn a certain region, uniform electric field E=−E0ˆk and magnetic field B=B0ˆk are present. At time t=0, a particle of mass m and charge q is given a velocity v=vj+vk. Find the minimum speed of the particle and the time when it happens so.
 View Solution
View SolutionElectric and magnetic field are directed as E0ˆi and B0ˆk, a particle of mass m and charge + q is released from position (0,2,0) from rest. The velocity of that particle at (x,5,0) is (5ˆi+12ˆj) the value of x will be
View SolutionThere exist uniform magnetic field →B=−B0ˆk in region of space with 0<x<d and 2d<x<3d as shown in the figure. A positive charged particle of mass m and charge q is projected with velocity →v=vˆi as shown in the figure. If radius of curvature of path of the charged particle in magnetic field isR(2d<R<3d) then time elapse by charged particle in magnetic field regions is
 View Solution
View Solution

