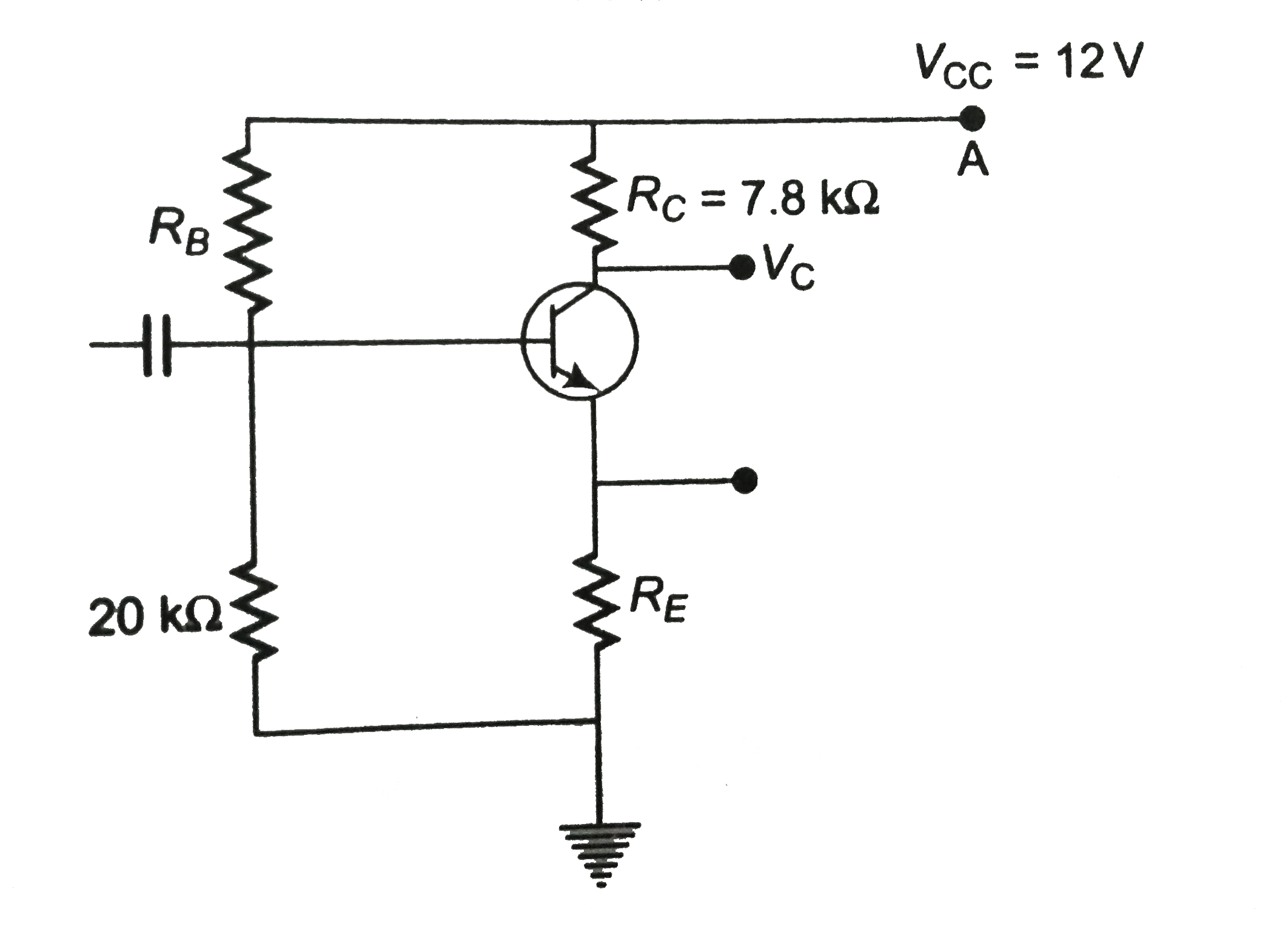
Passage I
An n-p-n transistor is used as a voltage amplifier in a commoin emitter circuit given
VC=8VIC=4mA
VCE=4V,
(VBE=0.6V,VBB=8V
βDc=200
The value of load resistqacne is
10 k ω
1 k ω
5 k ω
2.5 k ω
To find the value of the load resistance RL in the given n-p-n transistor circuit, we can follow these steps:
1. Identify the Given Values:
- VCC=8V
- IC=4mA=4×10−3A
- VCE=4V
- VBE=0.6V
- VBB=8V
- βDC=200
2. Apply Kirchhoff's Voltage Law (KVL):
In a common emitter configuration, we can apply KVL around the collector circuit. The equation can be expressed as:
VC=ILRL+VCE
Here, VC is the voltage at the collector, IL is the load current, and RL is the load resistance.
3. Rearranging the Equation:
We can rearrange the KVL equation to solve for RL:
RL=VC−VCEIL
4. Substituting Known Values:
We know that VC is equal to VCC in this case, so:
RL=VCC−VCEIC
Substituting the known values:
RL=8V−4V4×10−3A
5. Calculating RL:
RL=4V4×10−3A=44×10−3=1000Ω
6. Final Result:
Therefore, the load resistance RL is:
RL=1000Ω=1kΩ
Conclusion:
The value of the load resistance RL is 1kΩ.
---
- VCC=8V
- IC=4mA=4×10−3A
- VCE=4V
- VBE=0.6V
- VBB=8V
- βDC=200
In a common emitter configuration, we can apply KVL around the collector circuit. The equation can be expressed as:
VC=ILRL+VCE
Here, VC is the voltage at the collector, IL is the load current, and RL is the load resistance.
We can rearrange the KVL equation to solve for RL:
RL=VC−VCEIL
We know that VC is equal to VCC in this case, so:
RL=VCC−VCEIC
Substituting the known values:
RL=8V−4V4×10−3A
RL=4V4×10−3A=44×10−3=1000Ω
Therefore, the load resistance RL is:
RL=1000Ω=1kΩ
The value of the load resistance RL is 1kΩ.
Topper's Solved these Questions
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - COMPETION FILE (ASSERTION REASON TYPE QUESTIONS )
9 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - COMPETION FILE (MATCHING TYPE QUESTIONS )
2 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - COMPETION FILE (JEE(MAIN) & OTHER STATE BOARDS FOR ENGINEERING ENTRANCE )
31 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- WAVE OPTICALBOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - CHAPTER PRACTICE TEST
7 Videos
Similar Questions
Knowledge Check
Passage I
An n-p-n transistor is used as a voltage amplifier in a commoin emitter circuit given
VC=8VIC=4mA
VCE=4V,
(VBE=0.6V,VBB=8V
βDc=200
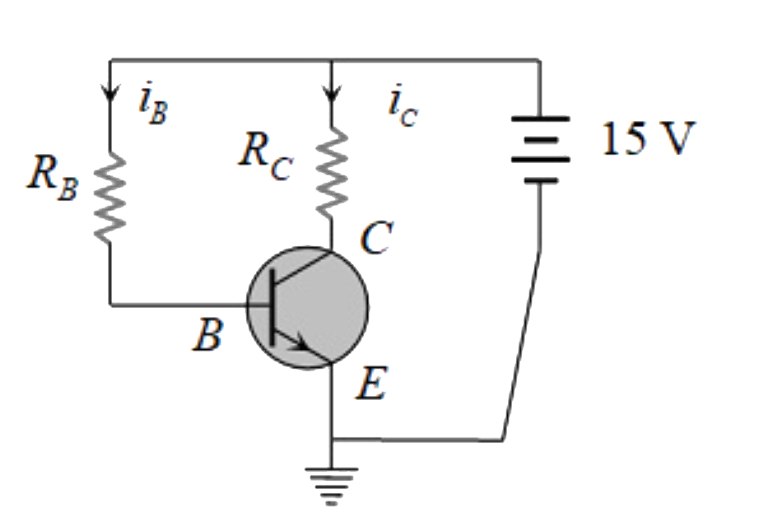
The value of base resistance isA185 k ωB275 k ωC370 k ωD410 k ωIn the following common emitter circuit if β=100,VCE=7V,VBE=Negligible, RC=2kΩ then IB=?
 A0.01mAB0.04mAC0.02mAD0.03mA
A0.01mAB0.04mAC0.02mAD0.03mA
In the junction transistor voltage amplifier circuit of figure, if R1=100kΩ,R2=1kΩ,VCC=6.0V and VBE=0.6V current gain=60AIB=54μABIC=3.24mACthe voltage across R2=3.24VDthe voltage across the collector-emitter=3.24V
In the following common emitter circuit , if β=100,VCE=7V,R(C)=2kΩandVBE negligible , then IB is
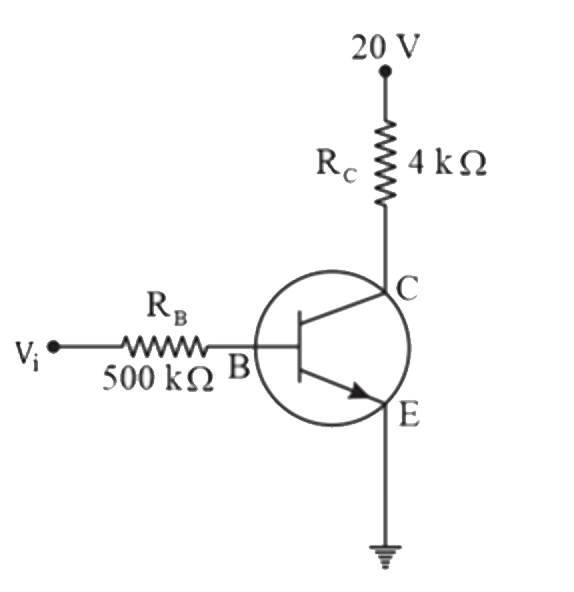
View SolutionIn the circuit shows in the figure, the input voltage
Vi is 20 V, VBE=0 and VCE=0. The values of lB,lC and β are given by
View SolutionAn n-p-n transistor in a common-emitter mode is used as a simple voltage-amplifier with a collector current of 4 mA. The terminals of a 8 V battery is connected to the collector through a load-resistance RL and to the base through a resistance RB. The collector-emitter voltage VCE=4V, the base-emitter voltage VBE=0.6V and the current amplification factor βdc=100. Then
View SolutionIn the circuit shown in the figure, the input voltage Vi is 20V, VBE=0 and VCE=0. The values of IB, IC and β are given by
View SolutionIn the circuit shown in the figure, the input voltage Vi is 20V,VBE=0 and VCE=0. The values of IB,IC and β are given by:
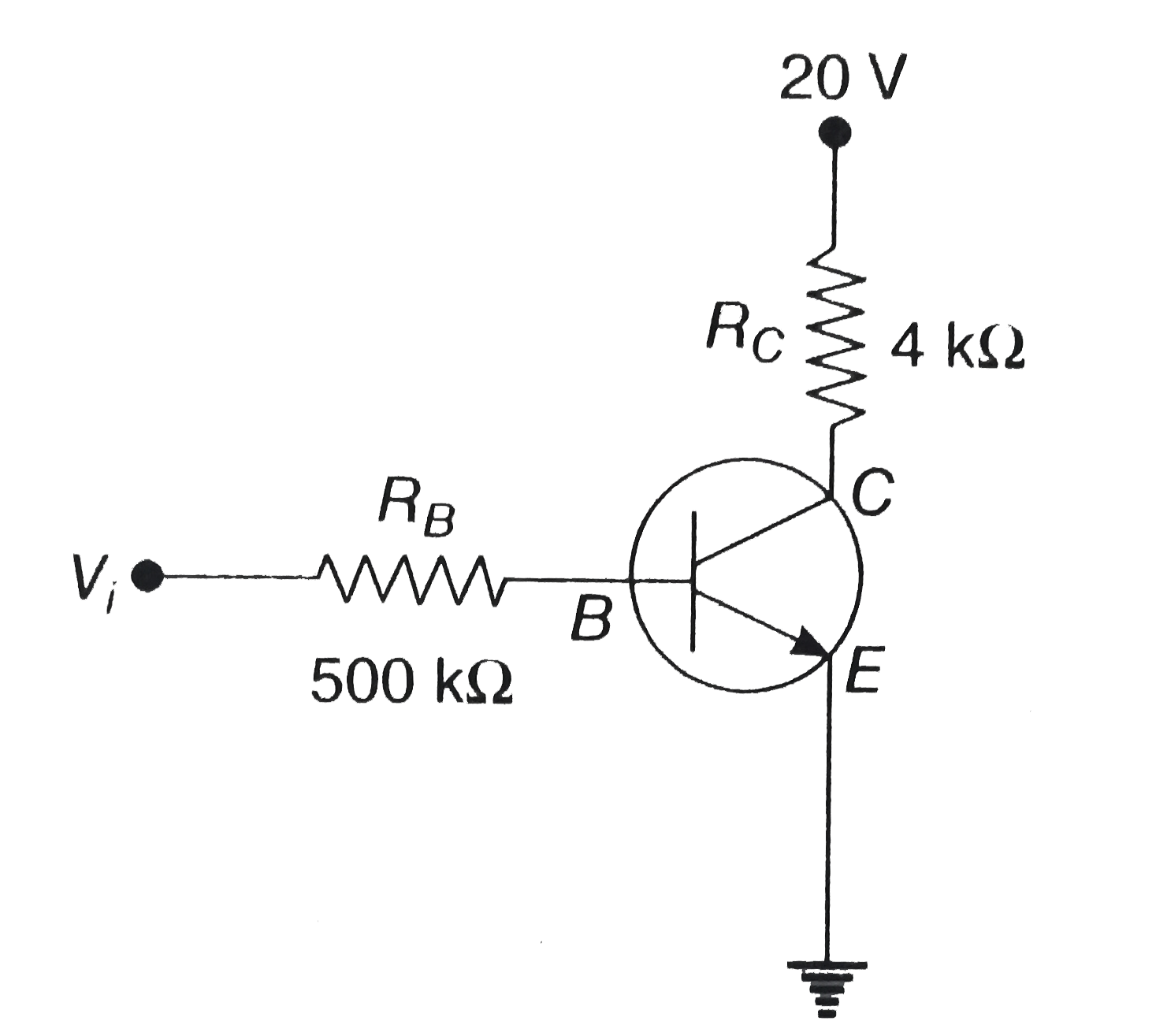
View Solution