An ideal gas in a thermally insulated vessel at internal pressure = P1, volume = V1 and absolute temperature = T1 expands irreversibly against zero external pressure, as shown in the diagram.The final internal pressure, volume and absolute temperature of gas are P2,V2 and T2, respectively.For this expansion,

q=0
T2=T1
P2V2=P1V1
P2Pγ2=P1Vγ1
The correct Answer is:A, B, C
Since the gas is thermally insulated, q = 0
Also, pext=0 hence w = 0
From first law of thermodynamics,
ΔU=q+w=0
∴ΔT=−orT2=T1
Applying ideal gas equation,
pV=nRT
As T is constant
p1V1=p2V2
Equation pV = constant is applicable only for the ideal gas in reversible adiabatic process. Hence, the relation.
p2Vγ2=p1Vγ1 is not applicable.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - MODERN PUBLICATIONCHAPTER - THERMODYNAMICSEXERCISE - Competition File (Matching Type Questions)
2 Videos
- THERMODYNAMICSBOOK - MODERN PUBLICATIONCHAPTER - THERMODYNAMICSEXERCISE - Competition File (Matrix Matching Type Questions)
4 Videos
- THERMODYNAMICSBOOK - MODERN PUBLICATIONCHAPTER - THERMODYNAMICSEXERCISE - Higher Order Thinking Questions
16 Videos
- STRUCTURE OF ATOMBOOK - MODERN PUBLICATIONCHAPTER - STRUCTURE OF ATOMEXERCISE - Unit Practice Test
13 Videos
Similar Questions
An ideal gas in a thermally insulated vessel at internal pressure = P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2andT2, respectively. For this expansion.
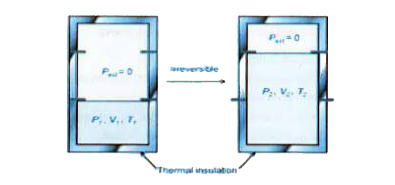
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
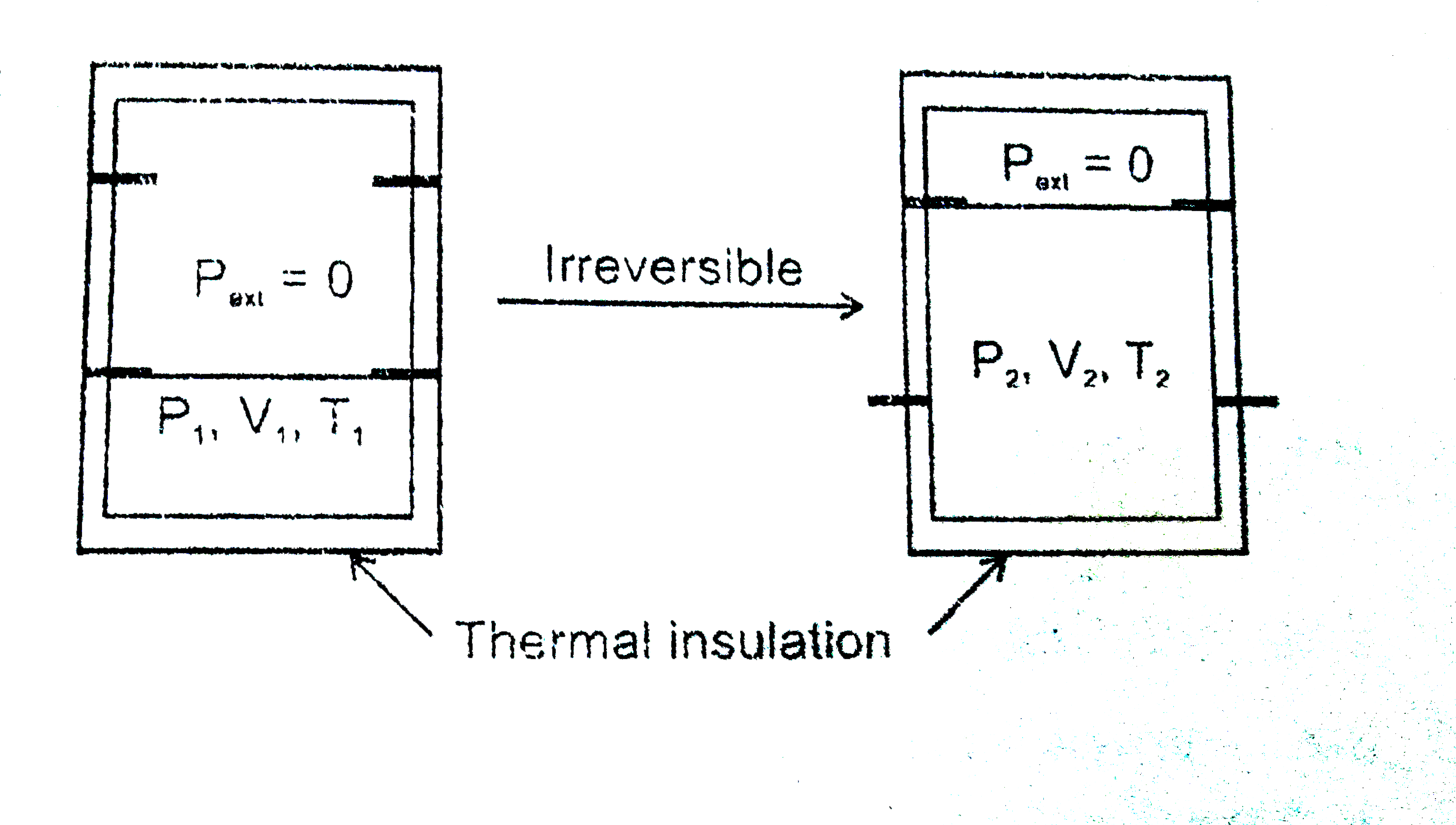
View Solution
Knowledge Check
An ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
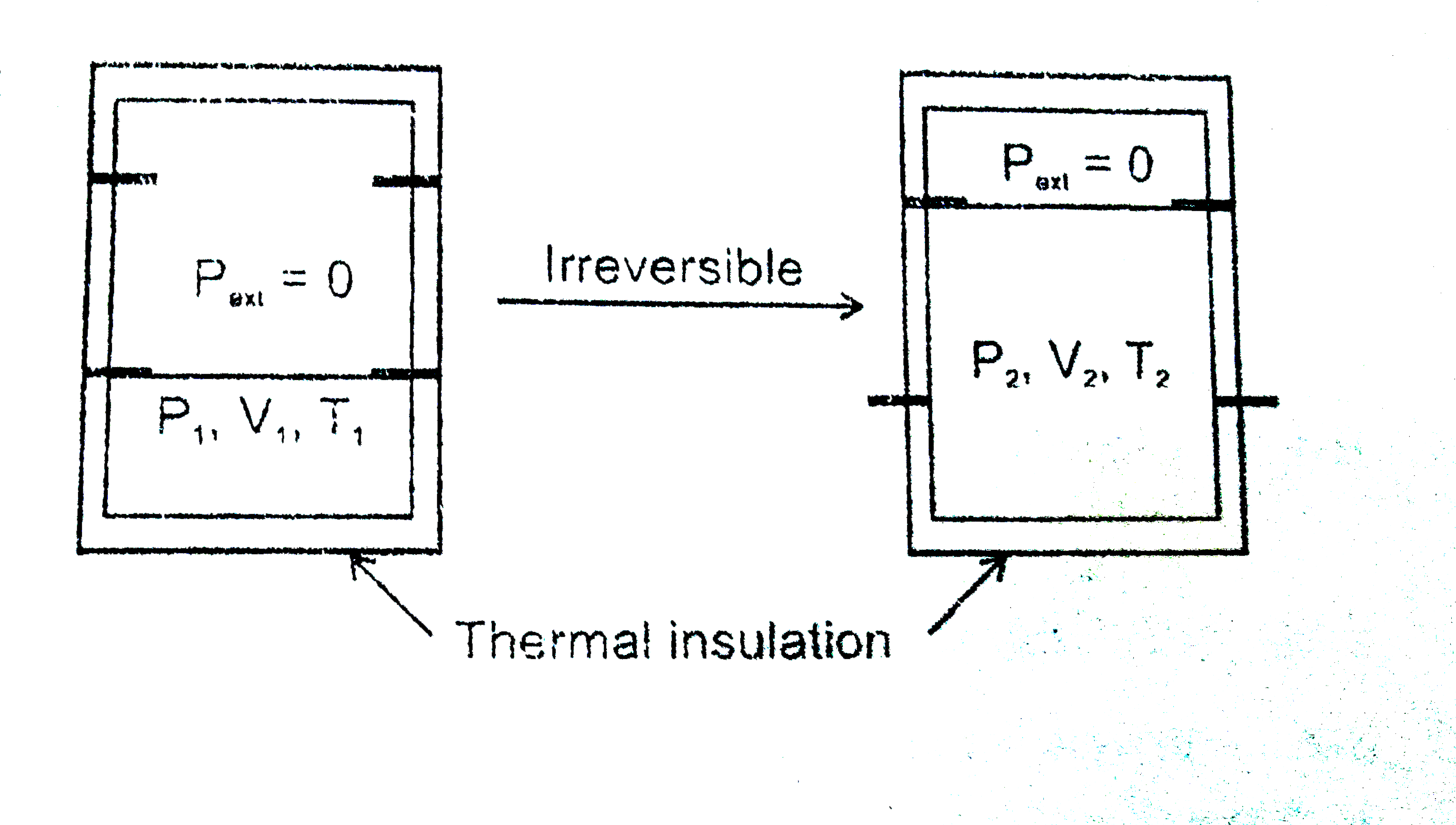 Aq=0BT2=T1CP2V2=PtV1DP2Vγ2=P1Vγ1
Aq=0BT2=T1CP2V2=PtV1DP2Vγ2=P1Vγ1An ideal gas in thermally insulated vessel at internal (pressure)=P1,(volume)=V1 and absolute temperature=T1 expands irreversiby against zero external, pressure , as shown in the diagram,
The final internal pressure, volume and absolute temperature of the gas are p2,V2andT2, respectively . For this expansion
 Aq=0BT2=T1Cp2V2=p1V1DP2Vγ2=P1Vγ2
Aq=0BT2=T1Cp2V2=p1V1DP2Vγ2=P1Vγ2Two containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
Ap1T2+p2T1T1×T2Bp1T2+p2T1T1+T2C12[p1T2+p2T1T1T2]Dp1T2−p2T1T1×T2]
An ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
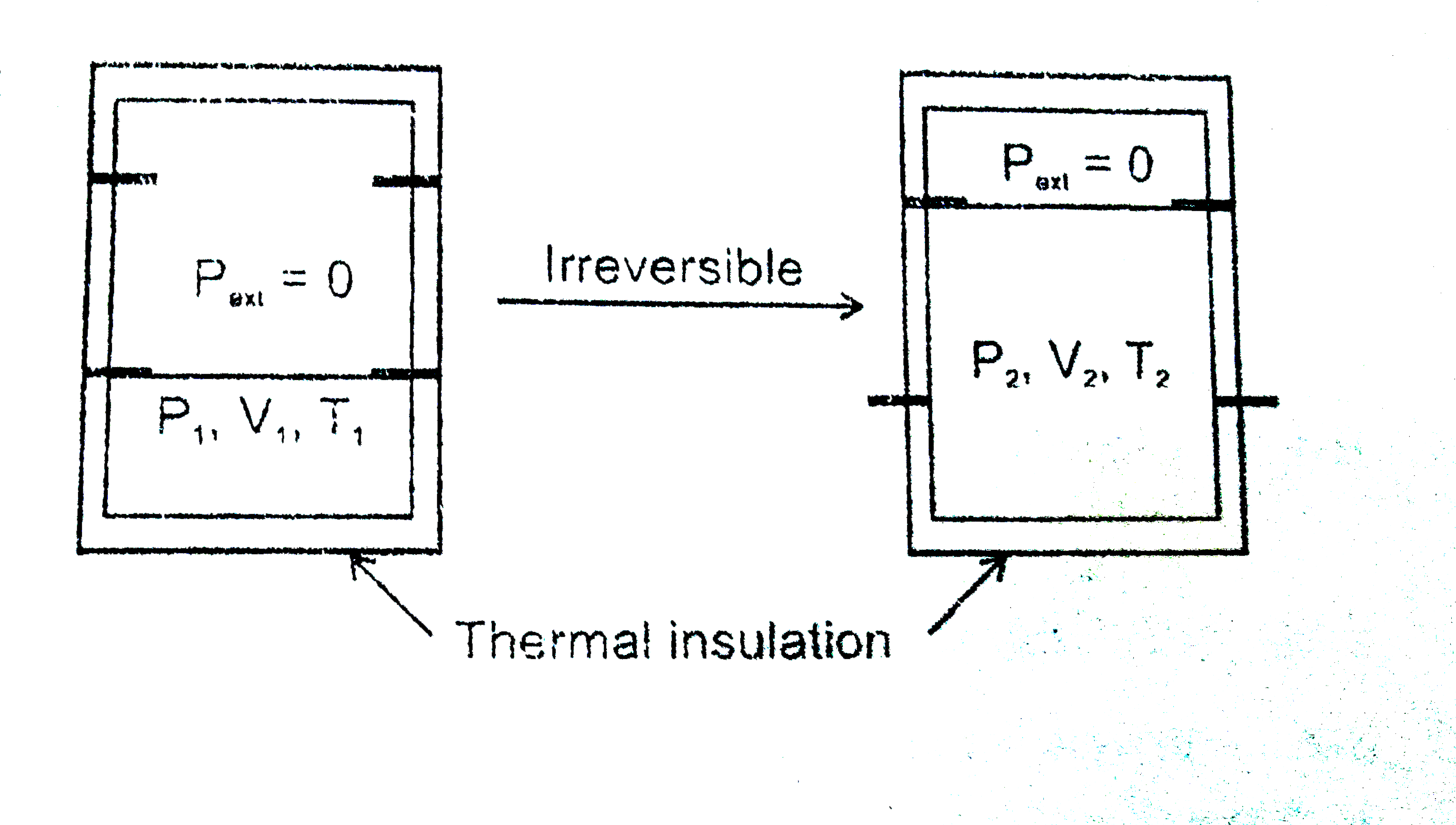
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionA gas enclosed in a vessel has pressure P, volume V and absolute temperature T, write the formula for number of molecule N of the gas.
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View Solution
