If AB||CD and the line EF cuts these lines at the points M and N, respectively. Bisectors of angles ∠BMNand∠MND meet at the point Q. Find the value of ∠MQN.
The correct Answer is:∠MQN=180∘−(∠QMN+∠MNQ)
Step by step video, text & image solution for If AB||CD and the line EF cuts these lines at the points M and N, respectively. Bisectors of angles angleBMN and angleMND meet at the point Q. Find the value of angleMQN. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - Fast Track Practice
104 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.1
45 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
In △ABC ,∠A=72∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=72∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के समद्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान ज्ञात करें |
View SolutionIn the given figure AB||CD and EF||DQ. Find the value of ∠DEF.
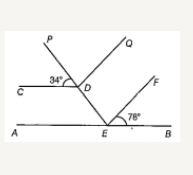
View Solution
Knowledge Check
In a triagle Δ ABC, the angle bisectors of ∠ABC and ∠ACB meet at point D and angle ∠BDC is 135∘ . Find the value of ∠BAC.
A45∘B75∘C60∘D90∘Two parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :A60∘B90∘C45∘D120∘Two parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :A60∘B90∘C45∘D120∘
In ΔABC,AB=AC and the bisectors of ∠B and ∠C meet AC and AB at point D and E respectively. Prove that BD=CE.
View SolutionTwo parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
View SolutionTwo parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
View SolutionAB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠BEF. If ∠LEB=35∘ ,then ∠CFQ will be :
View SolutionAB and CD are two parallel lines, PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠BEF. If ∠LEB=35∘ then ∠CFQ will be :
View Solution
