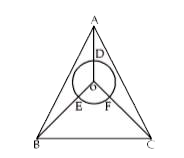
In an equilateral triangle ABC, AO, BO and CO are the angle bisectors meet at the incentre 'O'.D, E and F are the mid- points of AO, BO and CO respectively. A circle with centre 'O' passes through D, E and F. Area of the circle is 3πcm2. What is the perimeter of triangles (Δ)ABC?
12√3cm
18 cm
6√3cm
none of these
The correct Answer is:B
Step by step video, text & image solution for In an equilateral triangle ABC, AO, BO and CO are the angle bisectors meet at the incentre 'O'.D, E and F are the mid- points of AO, BO and CO respectively. A circle with centre 'O' passes through D, E and F. Area of the circle is 3pi cm^(2). What is the perimeter of triangles (Delta) ABC? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
Similar Questions
In ΔABC,DandE are the midpoint of AB and AC respectively. Find the ratio of the areas of ΔADEandΔABC.
 View Solution
View SolutionΔABC is an equilateral triangle and OB, OD and OC are angle bisector. D, E & F are midpoints of AO, BO and CO. 'O' is the centre of the circle in given figure. Area of circle is 3πcm2. Find the length of AB.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In an equilateral triangle ABC, AO, BO and CO are the angle bisectors meet at the incentre 'O'.D, E and F are the mid- points of AO, BO and CO respectively. A circle with centre 'O' passes through D, E and F. Area of the circle is 3πcm2. What is the perimeter of triangles (Δ)ABC?
A12√3cmB18 cmC6√3cmDnone of these - Question 2 - Select One
Area of ΔABC=30cm2. D and E are the mid - points of BC and AB respectively. Find A(ΔBDE) :
A10cm2B7.5cm2C15cm2Dnone of these - Question 3 - Select One or More
D,E and F are the middle points of the sides of the triangle ABC, then
Acentroid of the triangle DEF is the same as that of ABCBorthocentre of the traiangl DRF is the circumcentre of ABCCorthocentre of the triangle DEF is the incentre of ABCDcentroid of the triangle DEF is not the same as that of ABC
If D, E and F are the mid points of BC, CA and AB respectively of the △ABC then the ratio of aria parallelogram DEFB and area of the trapezium CAFD is ,
View SolutionIn a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
View SolutionIf D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :
View SolutionIf an equilateral triangle ABC is inscribed in a circle with centre O then the measure of ∠AOB is
View SolutionIn a triangle ABC, D, E, F are the mid-points of the sides BC, CA and AB respectively , the vector →AD is equal to
View Solution

