In a ΔABC, AB = AC and D is a point on AB, such that AD = DC = BC. Then, ∠BAC is
40∘
45∘
30∘
36∘
The correct Answer is:D
To solve the problem, we will follow these steps:
Step 1: Understand the triangle properties
Given that triangle ABC is isosceles with AB = AC, we know that the angles opposite to equal sides are also equal. Let's denote angle BAC as θ.
Step 2: Set up the angles
Since AB = AC, we have:
- ∠ABC=∠ACB=θ
Step 3: Use the triangle angle sum property
The sum of the angles in triangle ABC is 180 degrees:
∠BAC+∠ABC+∠ACB=180∘
Substituting the known angles:
θ+θ+∠BAC=180∘
This simplifies to:
2θ+∠BAC=180∘
Step 4: Express angle BAC in terms of theta
From the equation above, we can express angle BAC:
∠BAC=180∘−2θ
Step 5: Analyze triangle ACD
Since D is a point on AB such that AD = DC = BC, we can denote the length of these segments as x. In triangle ACD, since AD = DC, we have:
- ∠ACD=∠ADC
Step 6: Use the triangle angle sum property for triangle ACD
The sum of the angles in triangle ACD is also 180 degrees:
∠ACD+∠ADC+∠CAD=180∘
Since ∠ACD=∠ADC, we can denote them as ϕ:
ϕ+ϕ+∠CAD=180∘
This simplifies to:
2ϕ+∠CAD=180∘
Thus:
∠CAD=180∘−2ϕ
Step 7: Relate angles in triangle BCD
In triangle BCD, since BC = DC, we have:
- ∠BDC=∠BCD
Step 8: Use the triangle angle sum property for triangle BCD
The sum of the angles in triangle BCD is:
∠BCD+∠BDC+∠DBC=180∘
Let ∠BCD=ψ:
ψ+ψ+∠DBC=180∘
This simplifies to:
2ψ+∠DBC=180∘
Thus:
∠DBC=180∘−2ψ
Step 9: Relate angles and find the value of theta
From the previous steps, we can relate the angles:
1. ∠BAC=180∘−2θ
2. ∠ACD=180∘−2ϕ
3. ∠DBC=180∘−2ψ
Using the relationship between these angles and the fact that AD=DC=BC, we can derive that:
θ=72∘
Step 10: Calculate angle BAC
Substituting θ back into the equation for angle BAC:
∠BAC=180∘−2×72∘=180∘−144∘=36∘
Thus, the final answer is:
∠BAC=36∘
---
Given that triangle ABC is isosceles with AB = AC, we know that the angles opposite to equal sides are also equal. Let's denote angle BAC as θ.
Since AB = AC, we have:
- ∠ABC=∠ACB=θ
The sum of the angles in triangle ABC is 180 degrees:
∠BAC+∠ABC+∠ACB=180∘
Substituting the known angles:
θ+θ+∠BAC=180∘
This simplifies to:
2θ+∠BAC=180∘
From the equation above, we can express angle BAC:
∠BAC=180∘−2θ
Since D is a point on AB such that AD = DC = BC, we can denote the length of these segments as x. In triangle ACD, since AD = DC, we have:
- ∠ACD=∠ADC
The sum of the angles in triangle ACD is also 180 degrees:
∠ACD+∠ADC+∠CAD=180∘
Since ∠ACD=∠ADC, we can denote them as ϕ:
ϕ+ϕ+∠CAD=180∘
This simplifies to:
2ϕ+∠CAD=180∘
Thus:
∠CAD=180∘−2ϕ
In triangle BCD, since BC = DC, we have:
- ∠BDC=∠BCD
The sum of the angles in triangle BCD is:
∠BCD+∠BDC+∠DBC=180∘
Let ∠BCD=ψ:
ψ+ψ+∠DBC=180∘
This simplifies to:
2ψ+∠DBC=180∘
Thus:
∠DBC=180∘−2ψ
From the previous steps, we can relate the angles:
1. ∠BAC=180∘−2θ
2. ∠ACD=180∘−2ϕ
3. ∠DBC=180∘−2ψ
θ=72∘
Substituting θ back into the equation for angle BAC:
∠BAC=180∘−2×72∘=180∘−144∘=36∘
∠BAC=36∘
Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.1
45 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.2
100 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)
52 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
Knowledge Check
In ΔABC, AB=AC and D is a point on side AC such that BD = BC, If AB = 12.5 cm and BC = 5 cm, then what is the measure of DC ?
A2 cmB2.5 cmC3 cmD1.8 cmIn a ΔABC,AB=ACandAD⊥BC, then:
AAB<ADBAB>ADCAB=ADDAB≤ADIn ΔABC,∠B=2∠C. D is a point on side BC such that AD bisects ∠BACandAD=CD. Find the value of ∠BAC.
A36∘B72∘C108∘D120∘
In △ABC,AB>AC and D is any point on BC. Prove that, AB > AD.
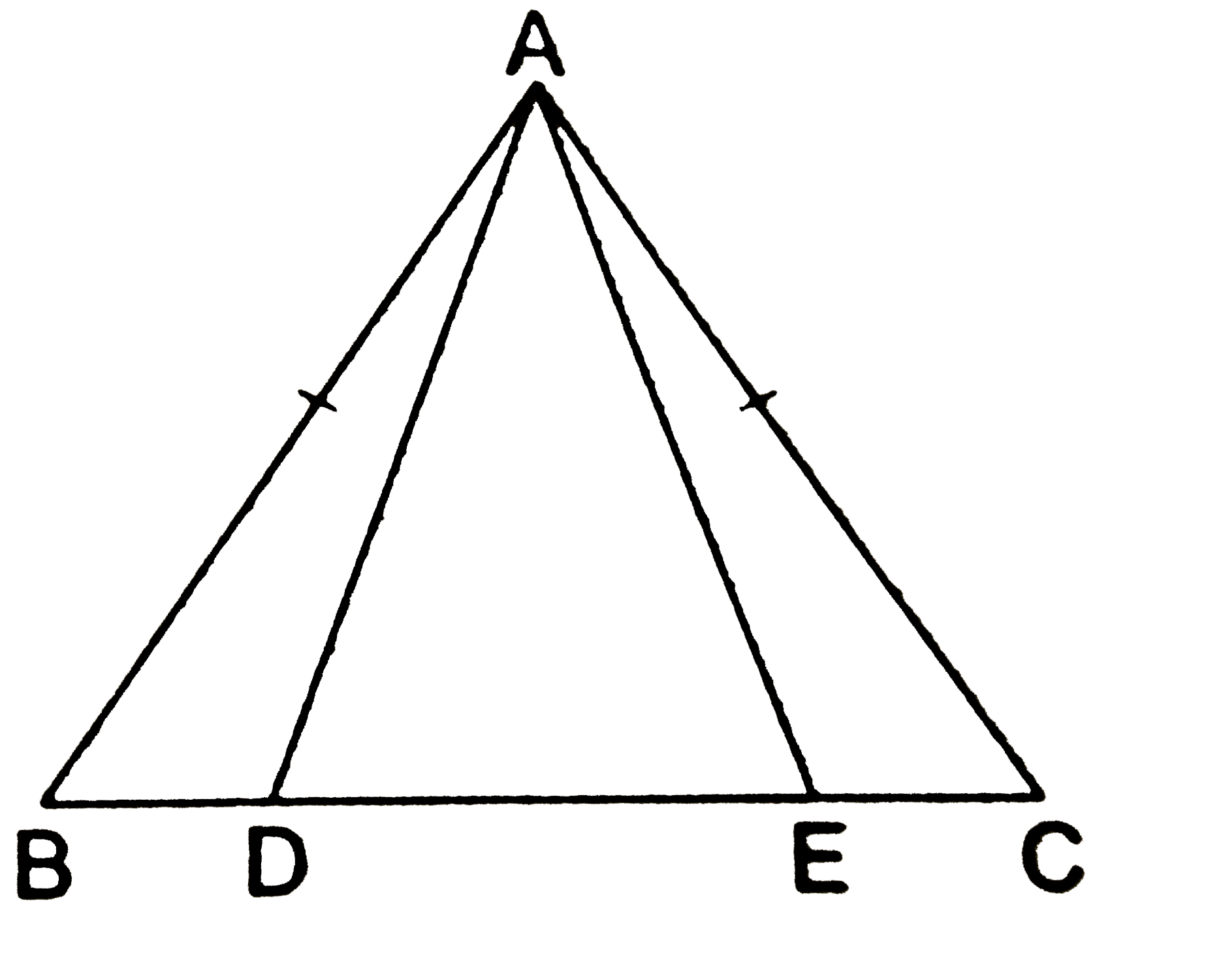
View SolutionIn an isosceles ΔABC with AB = AC, D and E are point on BC such that BE = CD. Show that AD = AE.
View SolutionIn a ΔABC,AB=AC,D is a point BC such that ∠BAD=50∘ and a point E on side AC such that AE =AD find ∠CDE
View SolutionIn △ABC, AB=AC and D is any point on BC, prove that AB2−AD2=BD.CD
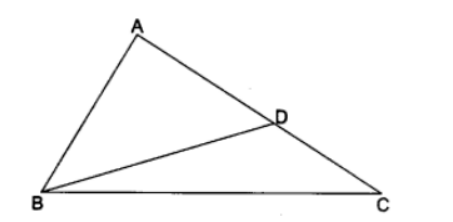
View SolutionIn Figure, AC>AB and D is the point on AC such that AB=AD. Prove that BC>CD
View Solution
