ABC is an equilateral triangle inscribed in a circle. D is any point on the arc BC. What is ∠ADB equal to?
90∘
60∘
45∘
None of these
The correct Answer is:B
To find the value of angle ADB in the given configuration, we can follow these steps:
1. Understanding the Configuration:
- We have an equilateral triangle ABC inscribed in a circle.
- D is a point on the arc BC of the circle, not including points B and C.
2. Properties of the Equilateral Triangle:
- In an equilateral triangle, all angles are equal to 60 degrees.
- Therefore, angle ABC = angle BCA = angle CAB = 60 degrees.
3. Identifying the Angles:
- We need to find angle ADB.
- Since D lies on the arc BC, we can use the property of angles subtended by the same arc.
4. Using the Inscribed Angle Theorem:
- The inscribed angle theorem states that the angle subtended by an arc at the center of the circle is twice the angle subtended at any point on the circumference.
- Therefore, angle BDC (the angle subtended by arc BC at point D) is equal to angle BAC (which is 60 degrees).
5. Finding Angle ADB:
- Since angle BDC = angle BAC = 60 degrees, and angle ADB is the same as angle BDC due to the inscribed angle theorem, we conclude that:
- Angle ADB = 60 degrees.
Final Answer:
Thus, the value of angle ADB is 60 degrees.
---
- We have an equilateral triangle ABC inscribed in a circle.
- D is a point on the arc BC of the circle, not including points B and C.
- In an equilateral triangle, all angles are equal to 60 degrees.
- Therefore, angle ABC = angle BCA = angle CAB = 60 degrees.
- We need to find angle ADB.
- Since D lies on the arc BC, we can use the property of angles subtended by the same arc.
- The inscribed angle theorem states that the angle subtended by an arc at the center of the circle is twice the angle subtended at any point on the circumference.
- Therefore, angle BDC (the angle subtended by arc BC at point D) is equal to angle BAC (which is 60 degrees).
- Since angle BDC = angle BAC = 60 degrees, and angle ADB is the same as angle BDC due to the inscribed angle theorem, we conclude that:
- Angle ADB = 60 degrees.
Thus, the value of angle ADB is 60 degrees.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.145videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.2100videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)52videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 240videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions18videos
HCF AND LCM
Similar Questions
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, then prove that PA is angle bisector of ∠BPC.
View SolutionAn equilateral triangle ABC and a scalene triangle DBC are inscribed in a circle on same side of the arc. What is ∠BDC equal to?
View Solution
Knowledge Check
- Question 1 - Select One
Area of an equilateral triangle inscribed in a circle of radius a is
A√3a2/4Bπa2/3C3√3a2/4D√3πa2/4 - Question 2 - Select One
An equilateral triangle is inscribed in a circle of radius 6 cm. Find its side.
A6√3B6√3C8√3D2√3 - Question 3 - Select One
If an equilateral triangle ABC is inscribed in a circle with centre O then the measure of ∠AOB is
A60∘B90∘C120∘D180∘
The area of an equilateral triangle inscribed in a circle of radius 4cm, is
View SolutionABC is an equilateral triangle inscribed in a circle of radius 4 cm. Find the area of the shaded portion.
 View Solution
View Solution[" An equilateral triangle "ABC" is inscribed in a circle.P is any point on the minor are BC.Prove "],[" that "PA=PB+PC]
View SolutionIn the given figure, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O, then the area of the shaded region is :
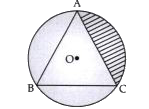 View Solution
View SolutionWhat is the area of an equilateral triangle inscribed in a circle of radius 4cm?
View Solution

