A, B and C are three points on a circle. The tangent at C meets BA extended at T. Given, ∠ATC=36∘and∠ACT=48∘, the angle subtended by AB at the centre of the circle is
84∘
48∘
96∘
72∘
The correct Answer is:C
To solve the problem step by step, we will follow the geometric principles involved with angles in circles and tangents.
1. Draw the Circle and Points:
- Draw a circle and mark three points A, B, and C on the circumference. Draw a tangent at point C that meets the line extended from AB at point T.
2. Label the Angles:
- According to the problem, we have:
- Angle ATC = 36°
- Angle ACT = 48°
3. Use the Alternate Segment Theorem:
- The Alternate Segment Theorem states that the angle subtended by a chord at the circumference is equal to the angle subtended by the same chord at the opposite segment. Therefore:
- Angle ABC = Angle ACT = 48°.
4. Find the Exterior Angle:
- In triangle ATC, angle BAC is the exterior angle. The exterior angle is equal to the sum of the two opposite interior angles:
- Angle BAC = Angle ATC + Angle ACT = 36° + 48° = 84°.
5. Find Angle ACB:
- Now, we need to find angle ACB. Since the angles in triangle ABC must sum up to 180°, we can find angle ACB:
- Angle ACB = 180° - Angle ABC - Angle BAC
- Angle ACB = 180° - 48° - 84° = 48°.
6. Find the Angle at the Center:
- The angle subtended by chord AB at the center (angle AOB) is twice the angle subtended at the circumference (angle ACB):
- Angle AOB = 2 × Angle ACB = 2 × 48° = 96°.
Final Answer:
The angle subtended by AB at the center of the circle is 96°.
---
- Draw a circle and mark three points A, B, and C on the circumference. Draw a tangent at point C that meets the line extended from AB at point T.
- According to the problem, we have:
- Angle ATC = 36°
- Angle ACT = 48°
- The Alternate Segment Theorem states that the angle subtended by a chord at the circumference is equal to the angle subtended by the same chord at the opposite segment. Therefore:
- Angle ABC = Angle ACT = 48°.
- In triangle ATC, angle BAC is the exterior angle. The exterior angle is equal to the sum of the two opposite interior angles:
- Angle BAC = Angle ATC + Angle ACT = 36° + 48° = 84°.
- Now, we need to find angle ACB. Since the angles in triangle ABC must sum up to 180°, we can find angle ACB:
- Angle ACB = 180° - Angle ABC - Angle BAC
- Angle ACB = 180° - 48° - 84° = 48°.
- The angle subtended by chord AB at the center (angle AOB) is twice the angle subtended at the circumference (angle ACB):
- Angle AOB = 2 × Angle ACB = 2 × 48° = 96°.
The angle subtended by AB at the center of the circle is 96°.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.145videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.2100videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)52videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 240videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions18videos
HCF AND LCM
Similar Questions
Knowledge Check
- Question 1 - Select One
A, B, C are three point on a circle. The tangent at A meets BC produced at T,∠BTA=40∘,∠CAT=44∘ . The angle subtended by BC at the centre of the circle is -
A84∘B92∘C96∘D104∘ - Question 2 - Select One
A, B and C are three points on a circle with centre O. The tangent at C meets BA produced to T. If ∠ATC=30∘ and ∠ACT=48∘, then what is the value of ∠AOB?
A78∘B96∘C102∘D108∘ - Question 3 - Select One
A, B and C are the three points on a circle such that ∠ABC=35∘and∠BAC=85∘. What is the angle (in degrees) subtended by arc AB at the centre of the circle?
A60B90C135D120
Theorem 10.8 : The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
View SolutionThe total plane angle subtended by a circle at its centre is
View SolutionIn figure , BOA is a diameter of circle and the tangent at point P meets BA produced at. T if ∠PBO=30∘ then ∠PTA=
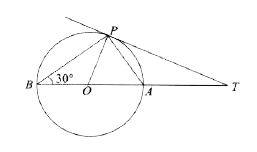 View Solution
View SolutionA,B and C are three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 90∘ and 110∘ respectively . Further suppose that the centre O lies on the interior ∠BAC. The ∠BAC is
View SolutionA, B and C are the three points on a circle such that the angle subtendsed by the chords AB and AC at the centre O are 90∘ and 110∘ respectively. ∠BAC is equal to
View Solution


