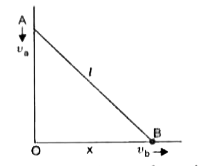
A rod of length 'l' rests at a point A against a smooth vertical wall while end B is on the floor as shown in the fig. If the end A moves uniformly downwards, what will be the velocity of the end B if x is the distance of point B from wall.
vB=√l2x2−1.va
√x2l2−1.va
l2−x2x.va
None of these
The correct Answer is:B
Let the position of point B be x at any instant such that dx OB = x and OA = y. The velocity of B. vb=dxdt is positive along x-axis while velocity of A va=dydt is constant and is down wards. There is a friction between rod floor at B. Now
x2+y2=l2
or 2xdxdt+2ydydt=0
or dxdt=v=−y/x(dydt)=y/x.va
As va is constant magnitude of the given downward velocity as .y. decreases with time.
Then vb=y/x.va
But y=√l2−x2
∴vb=√l2−x2x.va
Topper's Solved these Questions
- DESCRIPTION OF MOTION IN TWO AND THREE DIMENSIONBOOK - MODERN PUBLICATIONCHAPTER - DESCRIPTION OF MOTION IN TWO AND THREE DIMENSIONEXERCISE - MCQ(LEVEL-III)(Questions from AIEEE/ JEE Examinations)
6 Videos
- DESCRIPTION OF MOTION IN TWO AND THREE DIMENSIONBOOK - MODERN PUBLICATIONCHAPTER - DESCRIPTION OF MOTION IN TWO AND THREE DIMENSIONEXERCISE - RECENT COMPETITIVE QUESTIONS
7 Videos
- DESCRIPTION OF MOTION IN TWO AND THREE DIMENSIONBOOK - MODERN PUBLICATIONCHAPTER - DESCRIPTION OF MOTION IN TWO AND THREE DIMENSIONEXERCISE - Revision TEST
36 Videos
- DESCRIPTION OF MOTION IN ONE DIMENSION BOOK - MODERN PUBLICATIONCHAPTER - DESCRIPTION OF MOTION IN ONE DIMENSION EXERCISE - Revision Test
45 Videos
- E.M. INDUCTION AND A.C. CURRENTS BOOK - MODERN PUBLICATIONCHAPTER - E.M. INDUCTION AND A.C. CURRENTS EXERCISE - RECENT COMPETITIVE QUESTIONS
31 Videos
Similar Questions
A rod of length I leans by its upper end against a smooth vertical wall, while its other end leans against the floor. The end that leans against the wall moves uniformly downward. Then:
View SolutionA rod of length 'l' is inclined at an angle 'θ' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1, what is the velocity of end B at the instant when rod makes 'θ' angle with the horizontal.
View Solution
Knowledge Check
A rod of length I leans by its upper end against a smooth vertical wall, while its other end leans against the floor. The end that leans against the wall moves uniformly downward. Then:
 AThe other end also moves uniformlyBThe speed of other end goes on decreasingCThe speed of other end goes on increasingDThe speed of other end first decreases and then increases
AThe other end also moves uniformlyBThe speed of other end goes on decreasingCThe speed of other end goes on increasingDThe speed of other end first decreases and then increasesA uniform rod AB of length a hangs with one end against a smooth vertical wall, being supported by a string of length l, attached to the other end of the rod and to a point of the rod vertically above B. If the rod rests inclined to the wall at angle θ then cos2θ=
A(l2−a2)/a2B(l2−a2)/2a2C(l2−a2)/3a2Dnone of theseA light stick of length l rests with its one end against the smooth wall and other end against the smooth horizontal floor as shown in the figure. The bug starts at rest from point B and moves such that the stick always remains at rest. aP is the magnitude of acceleration of but of mass m, which depends upon its distance of x from the top end of the stick. Choose the correct option (s)
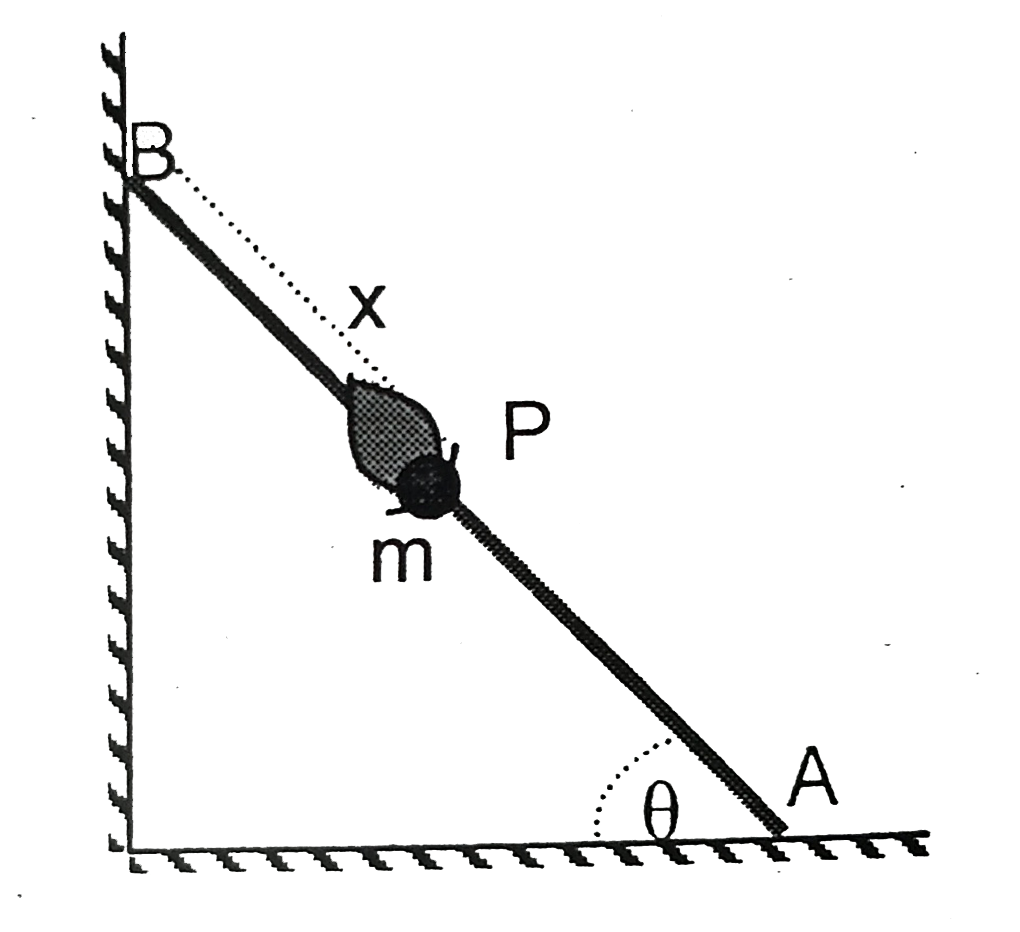 AaP=gsinθ(1−dl)BaP=gcosθ(1−xl)CThe time taken by the but to reach the bottom of the stick having started at the top end from rest is π2√lsinθ3gDThe time taken by the but to reach the bottom of the stick having started at the top end from rest is π2√lsinθ2
AaP=gsinθ(1−dl)BaP=gcosθ(1−xl)CThe time taken by the but to reach the bottom of the stick having started at the top end from rest is π2√lsinθ3gDThe time taken by the but to reach the bottom of the stick having started at the top end from rest is π2√lsinθ2
A rod of length 'l' is inclined at an angle 'theta' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1 what is the velocity of end B at the instant when rod makes 'theta' angle with the horizontal .
View SolutionA rod of length 'l' is inclined at an angle 'θ' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1, what is the velocity of end B at the instant when rod makes 'θ' angle with the horizontal.
View Solution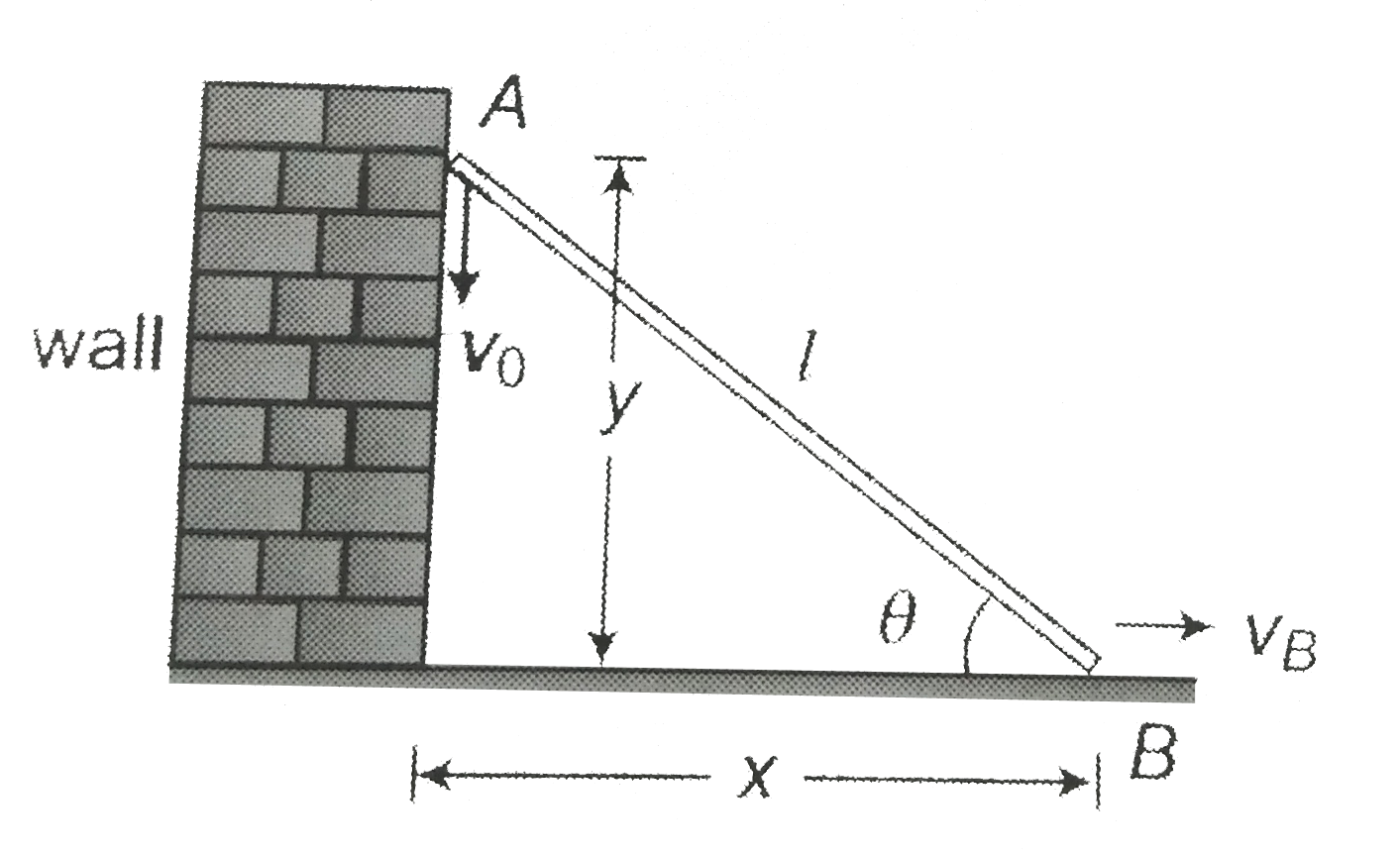
Consider a rod of length l resting on a wall and the floor. If the velocity of the upper end of a rod A is v0 in downward direction, find the velocity of the lower end B at this iinstant, when the rod makes an angle θ with horizontal
View SolutionA light stick of length l rests with its one end against the smooth wall and other end against the smooth horizontal floor as shown in the figure. The bug starts at rest from point B and moves such that the stick always remains at rest. aP is the magnitude of acceleration of but of mass m, which depends upon its distance of x from the top end of the stick. Choose the correct option (s)

View SolutionA rod of length l is released from the vertical position on a smooth horizontal plane. What is the nature of motion of the free end of the rod ?
View Solution
