A light beam is travelling from Region IV (figure). The refractive index in regions I, II and III and IV are n0,n02,n06andn08 respectively. The angle of incidence θ for which are beam just misses entering region IV is
sin−1(3/4)
sin−1(1/8)
sin−1(1/4)
sin−1(1/3)
The correct Answer is:B
(b)For refaction at parallel interfaces
n0sinθ=n02sinα=n06sin
β=n08sin90∘
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - MULTIPLE CHOICE QUESTION LEVEL - III16videos
RAY OPTICS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - RECENT COMPETITIVE QUESTION32videos
RAY OPTICS
- BOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - RECENT COMPETITIVE QUESTION32videos
RAY OPTICS
- BOOK - MODERN PUBLICATIONCHAPTER - PROPERTIES OF MATTEREXERCISE - RECENT COMPETITIVE QUESTIONS17videos
PROPERTIES OF MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - RCQ8videos
ROTATIONAL MOTION
Similar Questions
A light beam is traveling from Region I to region IV (refer figure). The refractive indices in Region I, II, III, and IV are n0,n0/2,n0/6andn0/8 , respectively. The angle of incidence θ for which the beam just misses entering Region IV is
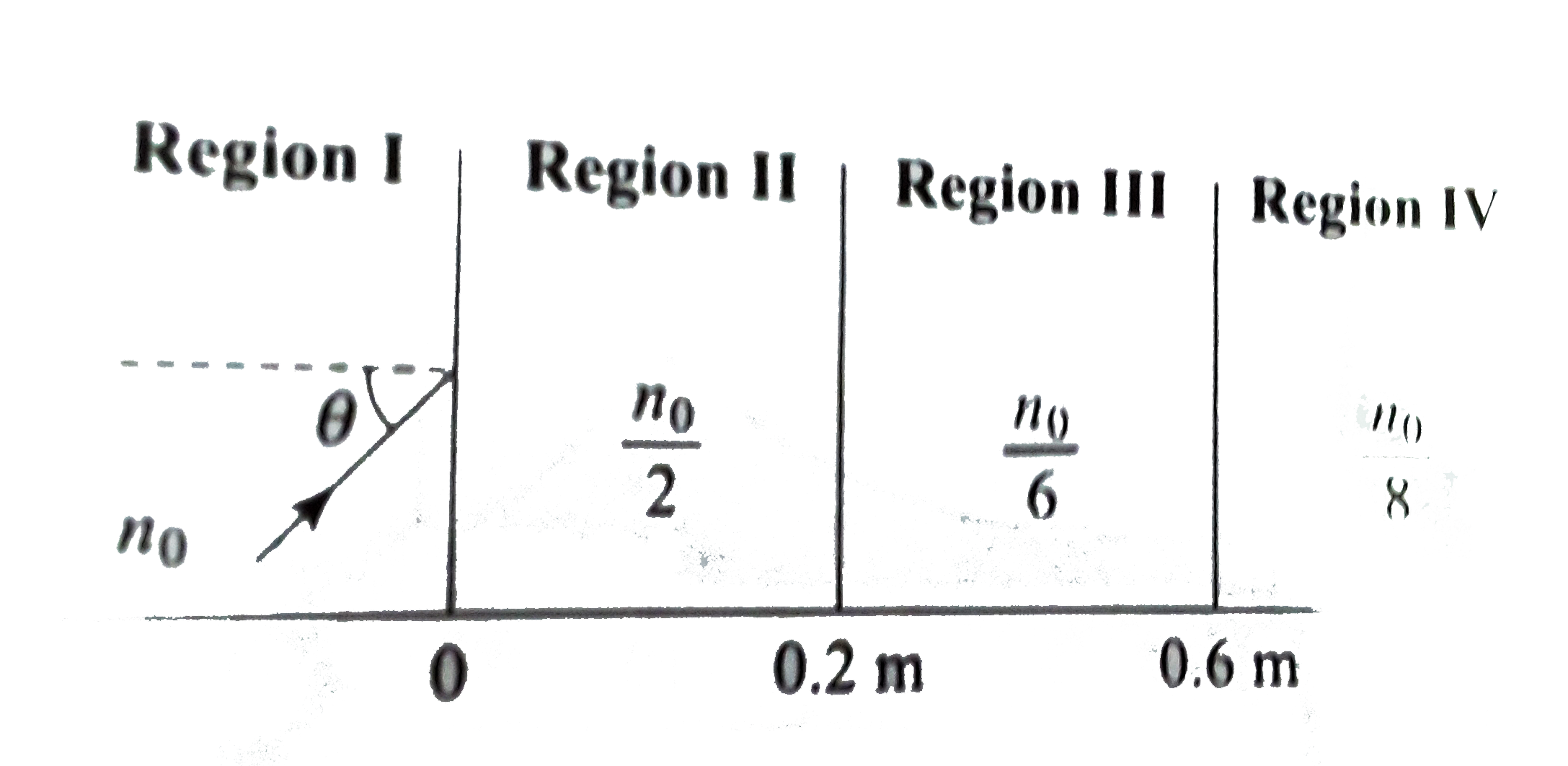
View SolutionAn intially parallel cyclindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0 and μ2 are positive constants and I is intensity of light beam. The intensity of the beam is decreasing with increasing radius.
Answer the following questions :
As the beam enters the medium, it willView Solution
Knowledge Check
- Question 1 - Select One
A light beam is travelling from Region I to IV (figure). The refractive index in regionals I,II,III and IV are n0=n02(n_0)/(6) and (n_0)/(8)respectively.The∠of∈cncethetaforwhichthebeamjustmissesenter∈gregionIVis−
Asin−1(34)Bsin−1(18)Csin−1(14)Dsin−1(13) - Question 2 - Select One
A light beam is traveling from Region I to region IV (refer figure). The refractive indices in Region I, II, III, and IV are n0,n0/2,n0/6andn0/8 , respectively. The angle of incidence θ for which the beam just misses entering Region IV is
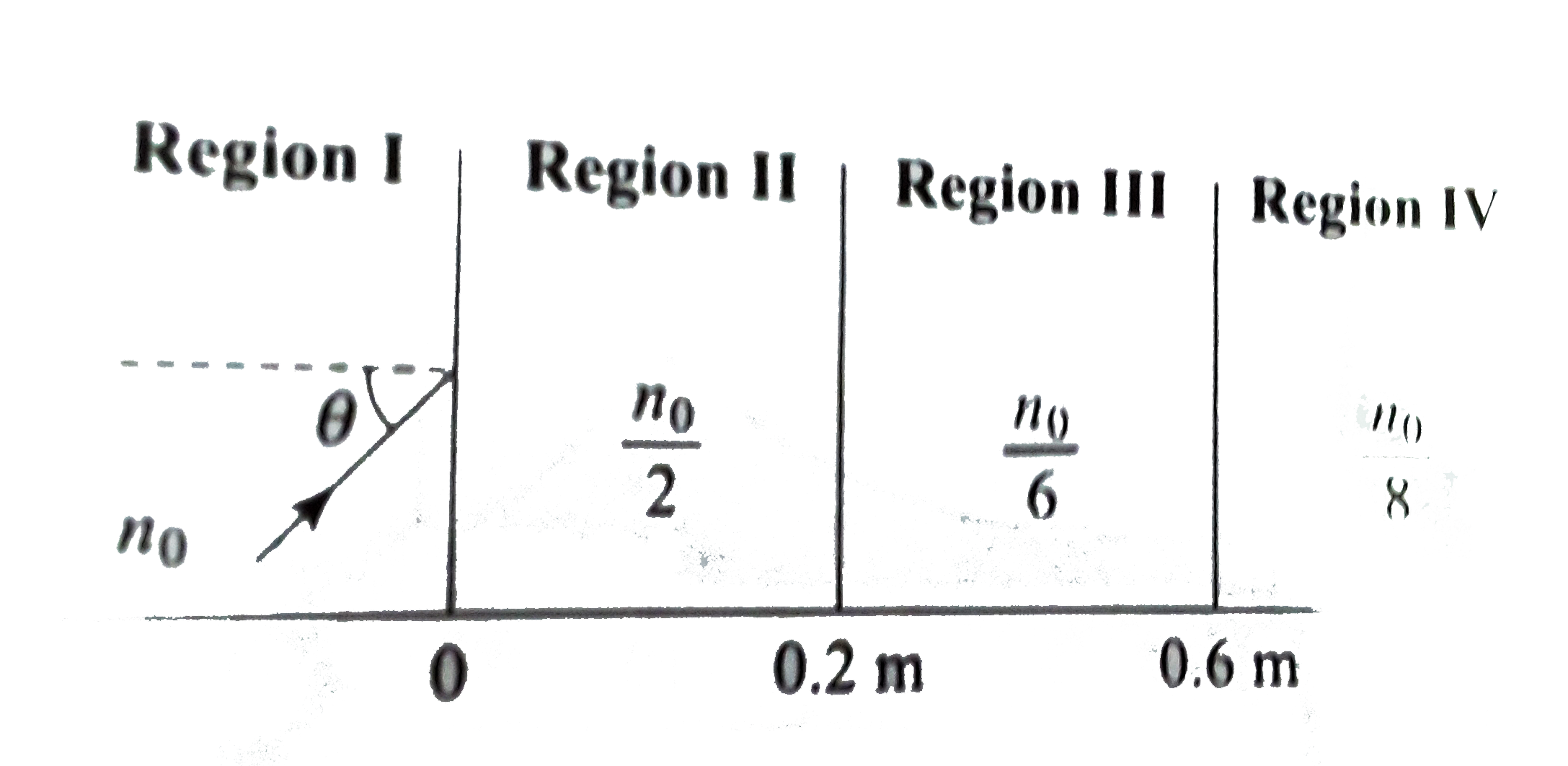Asin−1(3/4)Bsin−1(1/8)Csin−1(1/4)Dsin−1(1/3) - Question 3 - Select One
A ray of light passes from vacuum into a medium of refractive index n . If the angle of incidence is twice the angle of refraction , then the relation between the angle of incidence and the refractive index is
An=2sin(i2)Bn=2cos(i2)Cn=2tan(i2)Dn=12[cos(i2)]
Intensity of a light beam can be defined as amount of light energy incident in unit time on a unit area held normal to the direction of beam. A light beam of intensity I0 has a circular cross section of diameter d0. This beam is travelling in a medium of refractive index μ=√2and gets incident on the medium – air boundary at an angle of incidence i=30°. Assume that entire light energy gets transmitted into air. Find the intensity (I) of transmitted light beam.
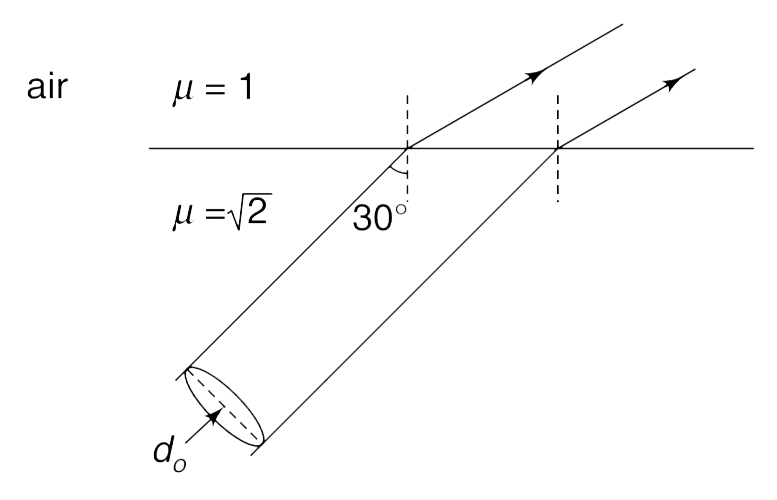
View SolutionA light ray enters into a medium whose refractive index varies along the x-axis as n(x)=n0√1+x4 where n0=1. The medium is bounded by the plates x=0,x=1 & y=0. It the ray enters at the origin at an angle 30∘ with x-axis
View SolutionFor a prism angle θ=600 the refractive indices of the left half and right half are resp, n1 and n2 (n2gen1) as shown in figure. The angle of incidence i is chosen such that the incident light rays will have minimum deviation if n1 = n2 = n = 1.5. For case of unequal refractive indices n1 = n and n2=n+∂at(n) the angle of emergence e=i+δ(e). Which of the following statement is/are correct?
View SolutionAn intially parallel cyclindrical beam travels in a medium of refractive index μ(I)=μ0+μ2I, where μ0 and μ2 are positive constants and I is intensity of light beam. The intensity of the beam is decreasing with increasing radius.
Answer the following questions :
As the beam enters the medium, it willView SolutionA light ray enters into a medium whose refractive index varies along the x-axis as n(x)=n0√1+x4 where n0=1. The medium is bounded by the plates x=0,x=1 & y=0. It the ray enters at the origin at an angle 30∘ with x-axis
View Solution
