A light of 6000Å is used to produce interference pattern.The observed fringe widht is 0.12 mm. The angle between two interfering wave trains is :
2×10−3 radian
3×10−3 radian
4×10−3 radian
5×10−3 radian.
The correct Answer is:D
Here β=λDd
Angle θ between two waves train is
θ=dD=λβ
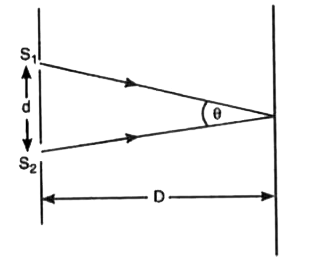
or θ=6000×10−100.12×10−3
=5×10−3 radian.
Topper's Solved these Questions
- WAVE OPTICS Book:MODERN PUBLICATIONChapter:WAVE OPTICS Exercise:MCQ LEVEL -1 (ASSERTIONS)
Explore 3 Videos
- WAVE OPTICS Book:MODERN PUBLICATIONChapter:WAVE OPTICS Exercise:MCQ LEVEL -1 (PARAGRAPH QUESTIONS )
Explore 34 Videos
- WAVE MOTIONBook:MODERN PUBLICATIONChapter:WAVE MOTIONExercise:RECENT COMPETITIVE QUESTIONS
Explore 18 Videos
- WORK , POWER , ENERGY AND COLLISIONSBook:MODERN PUBLICATIONChapter:WORK , POWER , ENERGY AND COLLISIONSExercise:Revision Test
Explore 40 Videos
Similar Questions
Sodium light (λ=6×10−7m) is used to produce interference pattern. The observed fringe width is 0.12 mm. The angle between two interfering wave trains, is
View SolutionIn a Young's double slit experiment, light of 500 nm is used to produce an interference pattern. When the distance between the slits is 0.05 mm, the angular width (in degree) of the fringes formed on the distance screen is close to:
View Solution
Knowledge Check
In a Young's double slit experiment, light of 500 nm is used to produce an interference pattern. When the distance between the slits is 0.05 mm, the angular width (in degree) of the fringes formed on the distance screen is close to:
A0.17∘B0.07∘C0.57∘D1.7∘In Young's double slit experiment, light of wavelength 6000Å is used to get an interference pattern on a screen. The fringe width changes by 1.5 mm, when the screen is brought towards the double slit by 50 cm. The distance between the two slits is
A0.2 mmB0.4 mmC0.6 mmD0.8 mmTwo slits separated by a distance of 0.5 mm are illuminated by light of wavelength 5000 Å. The interference fringes are obtained on a screen at a distance of 1.2 m. what is the phase difference between two interfering waves at a point 3 mm from the central bright fringe?
A7π radB3π radC5π radD4π rad
Two monochromatic light waves of equal intensities produce an interference pattern. At a point in the pattern, the phase difference between the interfering waves is π/2 rad. Express the intensity at this point as a fraction of the maximum intensity in the pattern.
View SolutionLaser light of wavelength 630 nm incident on a pair of slits produces an interference pattern in which the bright fringes are separated by 8.1 mm. a second light produces an interference pattern in which the fringes are separated by 7.2 mm. calculated the wavelength of the second light.
View SolutionLaser light of wavelength 630nm incident on a pair of slits produces an interference pattern where bright fringes are separated by 8.1mm. Another light produces the interference pattern, where the bright fringes are separated by 7.2mm. Calculate the wavelength of second light.
View SolutionLaser light of wavelength 630nm incident on a pair of slits produces an interference pattern where bright fringes are separated by 8.1mm. Another light produces the interference pattern, where the bright fringes are separated by 7.2mm. Calculate the wavelength of second light.
View SolutionTwo slits separated by a distance of 0.5 mm are illuminated by light of wavelength 5000 Å. The interference fringes are obtained on a screen at a distance of 1.2 m. what is the phase difference between two interfering waves at a point 3 mm from the central bbright fringe?
View Solution
