The minimum distance from centre of zero order maxima to where the intensity in half that at the centre is

A

$0.15 m m$

B

$0.20 m m$

C

$0.30 m m$

D

$0.40 m m$

Text Solution

Verified by Experts

The correct Answer is:A

$I = a^{2} + b^{2} + 2 a b cos θ, a = b$
$∴ I = 2 a^{2} (1 + cos θ) = 4 a^{2} \frac{{cos}^{2} (θ)}{2}$
$\Rightarrow I = I_{0} \frac{{cos}^{2} (θ)}{2}$
$∴ \frac{{cos}^{2} (θ)}{2} = \frac{I}{I_{0}} = \frac{1}{2}$ , " $\frac{cos θ}{2} = \frac{1}{\sqrt{2}}$
$∴ θ = 90^{\circ} = \frac{π}{2}$ radian.
$∴$ path difference $x = \frac{π}{2} \times \frac{λ}{2 π} = \frac{λ}{4}$
Distance of point from centre = $\frac{λ}{4} . \frac{D}{2 d}$
$= \frac{1}{4} \frac{D λ}{2 d} = \frac{1}{4} \times 6 m m = 0.15 m m$

|

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The distance of centre of mass from $O$ is

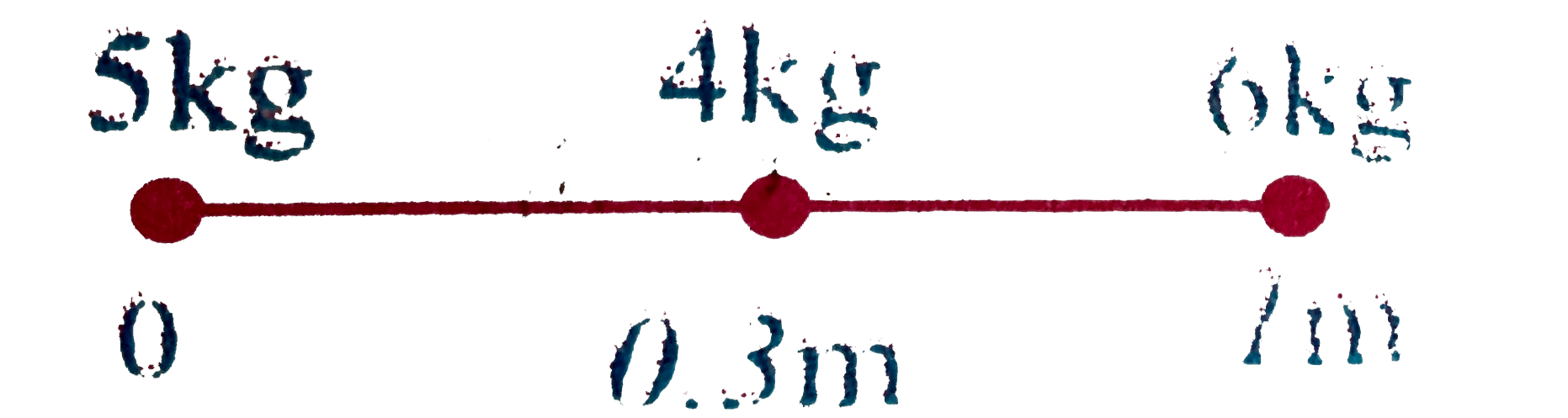A $0.21 m$
B $0.35 m$
C $0.42 m$
D $0.48 m$
Question 2 - Select One
Two identical coherent sources produce a zero order bright fringe on a screen. If $β$ is the band width, the minimum distance between two points on either side of the bright where the intensity is half that of maximum intensity is half of maximum intensity is
A $β / 2$
B $β / 4$
C $β / 3$
D $β / 6$
Question 3 - Select One
A circular current-carrying coil has a radius $R$ . The distance from the centre of the coil, on the axis, where $B$ will be $1 / 8$ of its value at the centre of the coil is
A $\frac{R}{\sqrt{3}}$
B $\sqrt{3} R$
C $2 \sqrt{3} R$
D $\frac{2 R}{\sqrt{3}}$

MODERN PUBLICATION-WAVE OPTICS -MCQ LEVEL -1 (PARAGRAPH QUESTIONS )

Home
Ask Doubt
Profile