Two beams, A and B, of plane polarized light with mutually perpendicular planes of polarization are seen through a polaroid. From the position when the beam A has maximum intensity (and beam B has zero intensity), a rotation of Polaroid through $30^{\circ}$ makes the two beams appear equally bright.If the initial intensities of the two beams are $I_{A}$ and $I_{B}$ respectively, then $\frac{I_{A}}{I_{B}}$ equals :

$\frac{1}{3}$

$\frac{3}{2}$

Text Solution

Verified by Experts

The correct Answer is:A

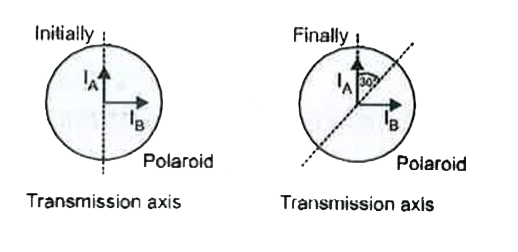
$I_{A} {cos}^{2} 30^{\circ} = I_{B} {cos}^{2} 60^{\circ}$
$I_{A} \frac{3}{4} = I_{B} \frac{1}{4}$ $\frac{I_{A}}{I_{B}} = \frac{1}{3}$

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Two beams A and B, of plane polarized light with mutually perpendicular planes of polarization are seen through a polaroid. From the position when the beam a has maximum intensity (and beam B has zero ntensity), a rotation of polaroid through $30^{\circ}$ makes the two beams appear equally bright. If the initial intensities of the two beams are $I_{A}$ and $I_{B}$ respectively, then $\frac{I_{A}}{I_{B}}$ equals:
A3
B $\frac{3}{2}$
C1
D $\frac{1}{3}$
Question 2 - Select One
Two beams A and B, of plane polarized light with mutually perpedicular planes of polarization are seen through a polaroid. From the position where the beam A has maximum intensity and the other beam B has zero intensity , the polaroid is rotated through $30^{\circ}$ making the two beams appear equally bright. If the initial intensities of the two beams are $I_{A}$ and $I_{B 0}$ respectively, then $\frac{I_{A}}{I_{B}}$ equals
A2
B $3 / 2$
C $1$
D $1 / 3$
Question 3 - Select One
Two beams, A and B, of plane polarised light with mutually perpendicular planes of polarisation are seen through a polarised light with mutually perpendicular planes of polarisation are seen through a polaroid. From the position when the beam A has maximum intensity (and beam B has zero intensity). a rotation of Polaroid through $30^{\circ}$ makes the two beams appear equally bright. If the intiial intensities of the two beams are $I_{A} and I_{B}$ respectively, then $I_{A} / I_{B}$ equals :
A $1 / 3$
B $3$
C $3 / 2$
D $1$

MODERN PUBLICATION-WAVE OPTICS -MCQ LEVEL - III

Home
Ask Doubt
Profile

The correct Answer is:A

IAcos230∘=IBcos260∘ IA34=IB14 IAIB=13

Topper's Solved these Questions

Similar Questions

Knowledge Check

MODERN PUBLICATION-WAVE OPTICS -MCQ LEVEL - III

$I_{A} {cos}^{2} 30^{\circ} = I_{B} {cos}^{2} 60^{\circ}$
$I_{A} \frac{3}{4} = I_{B} \frac{1}{4}$ $\frac{I_{A}}{I_{B}} = \frac{1}{3}$