Given P(x)=x4+ax3++bx2+cx+d such that x=0 is the only real root of p''(x)=0. If P(−1)<P(1), then in the interval [-1, 1] :
P(-1) is the minimum and P(1) is the maximum of P
P(-1) is not the minimum and P(1) is the maximum of P
P(-1) is the minimum but P(1) is not the maximum of P
neither P(−1) is the minimum nor P(1) is the maximum of P.
The correct Answer is:B
Topper's Solved these Questions
- APPLICATION OF DERIVATIVES BOOK - MODERN PUBLICATIONCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - Latest Questions from AIEEE/JEE Examinations
13 Videos
- APPLICATION OF DERIVATIVES BOOK - MODERN PUBLICATIONCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - Recent Competitive Questions (Questions from Karnataka CET & COMED)
25 Videos
- APPLICATION OF DERIVATIVES BOOK - MODERN PUBLICATIONCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - Recent Competitive Questions (Questions from Karnataka CET & COMED)
25 Videos
- AREA UNDER CURVES BOOK - MODERN PUBLICATIONCHAPTER - AREA UNDER CURVES EXERCISE - Recent Competitive Questions (Question from karnataka CET & COMED)
9 Videos
Similar Questions
Given P(x)=x4+ax3+cx+d such that x=0 is the only real root of P'(x)=0.IfP(1)<P(1) , then in the interval [1,1] . (1) P(1) is the minimum and P(1) is the maximum of P (2) P(1) is not minimum but P(1) is the maximum of P (3) P(1) is the minimum but P(1) is not the maximum of P (4) neither P(1) is the minimum nor P(1) is the maximum of P
View SolutionIf P(x)=x4+ax3+bx2+cx+d,P(1)=P2=P(3)=0 then find P(4)
View Solution
Knowledge Check
Given P(x) =x4+ax3+bx2+cx+d such that x=0 is the only real root of P'(x) =0 . If P(-1) < P(1), then in the interval [−1,1]
AP(-1) is the minimum and P(1) is the maximum of PBP(-1) is not minimum but P (1)is the maximum of PCP(-1) is the minimum and P(1) is not the maximum of PDneither P(-1) is the minimum nor P(1) is the maximum of PGiven P(x) =x4+ax3+bx2+cx+d such that x=0 is the only real root of P'(x) =0 . If P(-1) lt P(1),then∈the∫erval[-1,1]
A(a) P(-1) is the minimum and P(1) is the maximum of PB(b) P(-1) is not minimum but P(1) is the maximum of PC(c) P(-1) is not minimum and P(1) is not the maximum of PD(d) neither P(-1) is the minimum nor P(1) is the maximum of PIf x2+x+1 is a factor of ax3+bx2+cx+d, then the real root of ax3+bx2+cx+d=0 is
A−d/aBd/aCa/dDnone of these
Let P(x)=x4+ax3+bx2+cx+d, where a,b,c,d∈R . Suppose P(0)=6,P(1)=7,P(2)=8 and P(3)=9, then find the value of P(4)
View SolutionLet P(x)=x4+ax3+bx2+cx+d, where a,b,c,d∈R. Suppose P(0)=6,P(1)=7,P(2)=8 and P(3)=9, then find the value of P(4)
View SolutionLet P(x)=x4+ax3+bx2+cx+d, where a,b,c,d∈R.Suppose P(0)=6,P(1)=7,P(2)=8andP(3)=9, then find the value of P(4).
View SolutionLet P(x)=x4+ax3+bx2+cx+d be a polynomial such that P(1)=1,P(2)=8,P(3)=27,P(4)=64 then find P(10)
View SolutionIn the given figure graph of y=p(x)=x4+ax3+bx2+cx+d is given
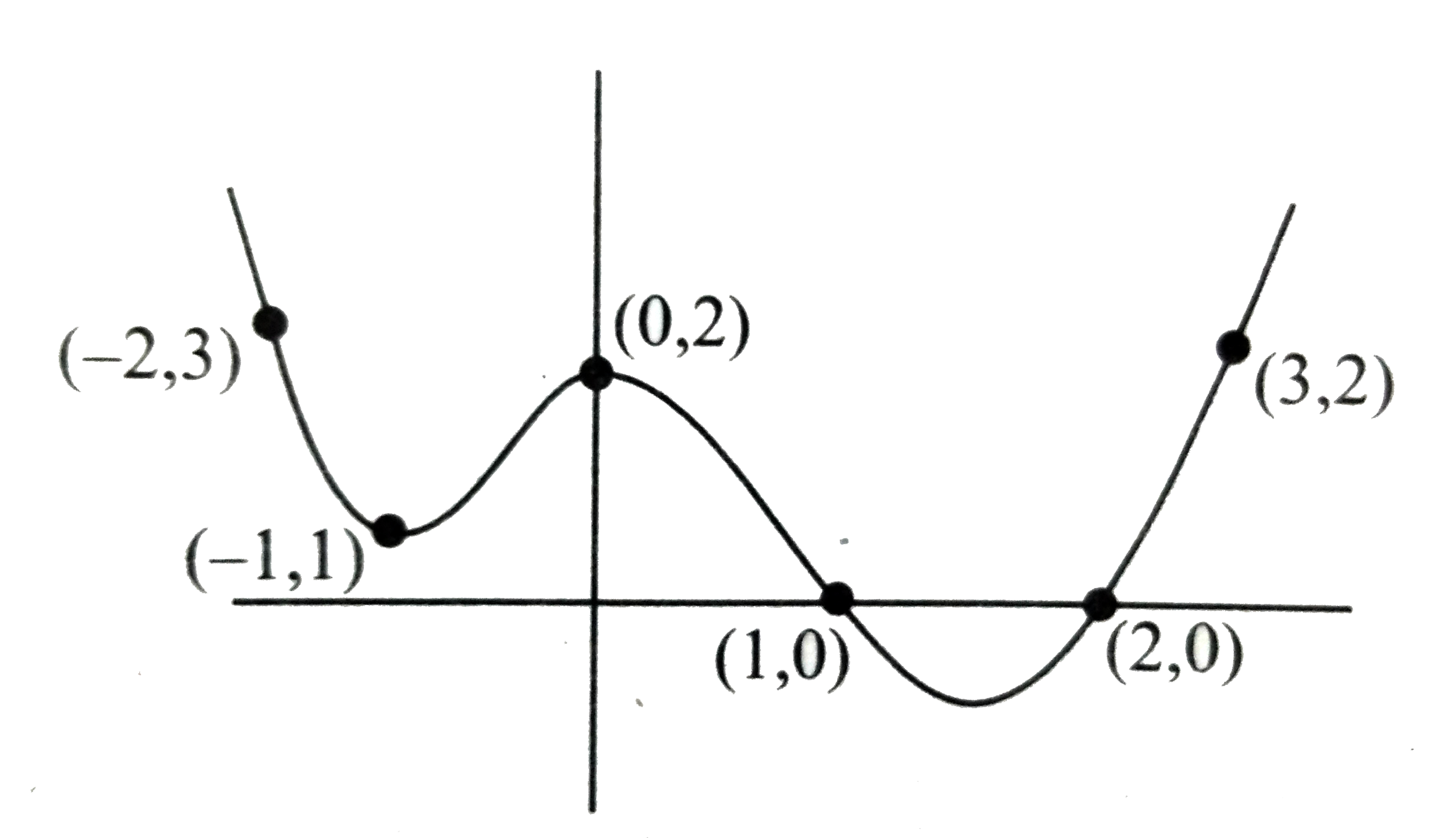
The product of all imaginery roots of p(x)=(0) is
View Solution
