A rectangle and a parallelogram have equal areas. If the sides of the rectangle are 10 m and 12 m and the base of the parallelogram is 20 m, then the altitude of the parallelogram is (a) 3 m (b) 5 m (c) 6 m (d) 7 m
To find the altitude (height) of the parallelogram given that it has the same area as a rectangle, we can follow these steps:
Step 1: Calculate the area of the rectangle.
The area A of a rectangle is given by the formula:
A=length×breadth
In this case, the length is 10 m and the breadth is 12 m.
A=10m×12m=120m2
Step 2: Set up the area formula for the parallelogram.
The area A of a parallelogram is given by the formula:
A=base×height
Here, the base of the parallelogram is given as 20 m. Let the height be h.
A=20m×h
Step 3: Set the areas equal to each other.
Since the areas of the rectangle and the parallelogram are equal:
120m2=20m×h
Step 4: Solve for the height h.
To find h, we can rearrange the equation:
h=120m220m=6m
Conclusion:
The altitude (height) of the parallelogram is 6m.
Final Answer:
(c) 6 m
---
The area A of a rectangle is given by the formula:
A=length×breadth
In this case, the length is 10 m and the breadth is 12 m.
A=10m×12m=120m2
The area A of a parallelogram is given by the formula:
A=base×height
Here, the base of the parallelogram is given as 20 m. Let the height be h.
A=20m×h
Since the areas of the rectangle and the parallelogram are equal:
120m2=20m×h
To find h, we can rearrange the equation:
h=120m220m=6m
The altitude (height) of the parallelogram is 6m.
(c) 6 m
Topper's Solved these Questions
Similar Questions
The area of a parallelogram and a square are the same.If the perimeter of the square is 160 m and the height of the parallelogram is 20 m ,find the length of the corresponding base of the parallelogram.
View SolutionThe given figure shows a parallelogram of 20 m height. The base of the parallelogram is 40 m long.
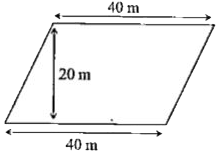
What is the area of the parallelogram?
View Solution
Knowledge Check
A rectangle and a parallelogram have equal areas. If the sides of a rectangle are 10 m and 12 m and the base of the parallelogram is 20 m, then the altitude of the parallelogram is
A7 mB6 mC5 mD3 mA triangle and a parallelogram are constructed on the same base such that their areas are equal. If the altitude of the parallelogram is 100m, then the altitude of the triangle is 10√2m (b) 100m (c) 100√2m (d) 200m
A100 mB200 mC100√2 mD10√2 mA parallelogram and a square have the same area. If the sides of the square measure 40 m and corresponding base of the parallelogram.
A44 mB54 mC64 mD74 m
Find the areas of the rectangles whose sides are :
12 m and 21 m
View SolutionA rectangle and a parallelogram have equal areas. The base of the parallelogram is 20 cm and the altitude is 6 cm. Which one of the following cannot be the ratio of dimensions of the rectangle ?
View SolutionIf a rectangle and a parallelogram are equal in area and have the same base and are situated on the same side, then the ratio of perimeter of rectangle and that of parallelogram is k, then k is :
View SolutionIf a rectangle and a parallelogram are equal in area and have the same base and are situated on the same side, then the quotient: Perimeter of rectanglePerimeter of parallelogram is -
View SolutionThe side of a rectangle are 6.01 m and 12 m Taking the significant figures into account , the area of the rectangle is
View Solution
