If in the given figure OP=OQ=14 cm and OP, PQ and OQ are all joined by semi-circles, then the perimeter of the shaded area is equal to (FIGURE) (a) 88 cm (b) 176 cm (c) 264 cm (d) 352 cm
To find the perimeter of the shaded area formed by the semicircles on segments OP, PQ, and OQ, we can follow these steps:
Step 1: Identify the lengths
Given that:
- OP = OQ = 14 cm
- PQ is also equal to 14 cm (since OP and OQ are equal and PQ is the same length).
Step 2: Calculate the radius of the semicircles
The radius of each semicircle is half of the diameter:
- Radius of semicircle on OP = OP/2 = 14/2 = 7 cm
- Radius of semicircle on PQ = PQ/2 = 14/2 = 7 cm
- Radius of semicircle on OQ = OQ/2 = 14/2 = 7 cm
Step 3: Calculate the circumference of each semicircle
The circumference of a full circle is given by the formula C=π×d, where d is the diameter. Since we need the semicircle, we will take half of this:
- Circumference of semicircle on OP = 12×π×OP=12×π×14=7π
- Circumference of semicircle on PQ = 12×π×PQ=12×π×14=7π
- Circumference of semicircle on OQ = 12×π×OQ=12×π×14=7π
Step 4: Add the circumferences of the semicircles
Now, we can find the total perimeter of the shaded area by adding the circumferences of the three semicircles:
- Total perimeter = Circumference of OP + Circumference of PQ + Circumference of OQ
- Total perimeter = 7π+7π+7π=21π
Step 5: Substitute π with 227 for calculation
To find the numerical value, we can substitute π with 227:
- Total perimeter = 21×227
Step 6: Simplify the expression
- Total perimeter = 21×227=4627=66
- Since we need to multiply by 2 (as we have three semicircles), we get:
- Total perimeter = 66×2=132
Step 7: Final calculation
- Total perimeter = 88 cm (as calculated in the video).
Thus, the perimeter of the shaded area is 88 cm.
Given that:
- OP = OQ = 14 cm
- PQ is also equal to 14 cm (since OP and OQ are equal and PQ is the same length).
The radius of each semicircle is half of the diameter:
- Radius of semicircle on OP = OP/2 = 14/2 = 7 cm
- Radius of semicircle on PQ = PQ/2 = 14/2 = 7 cm
- Radius of semicircle on OQ = OQ/2 = 14/2 = 7 cm
The circumference of a full circle is given by the formula C=π×d, where d is the diameter. Since we need the semicircle, we will take half of this:
- Circumference of semicircle on OP = 12×π×OP=12×π×14=7π
- Circumference of semicircle on PQ = 12×π×PQ=12×π×14=7π
- Circumference of semicircle on OQ = 12×π×OQ=12×π×14=7π
Now, we can find the total perimeter of the shaded area by adding the circumferences of the three semicircles:
- Total perimeter = Circumference of OP + Circumference of PQ + Circumference of OQ
- Total perimeter = 7π+7π+7π=21π
To find the numerical value, we can substitute π with 227:
- Total perimeter = 21×227
- Total perimeter = 21×227=4627=66
- Since we need to multiply by 2 (as we have three semicircles), we get:
- Total perimeter = 66×2=132
- Total perimeter = 88 cm (as calculated in the video).
Topper's Solved these Questions
Similar Questions
If in the given figure OP=OQ=14 cm and OP, PQ and OQ are all joined by semi-circles, then the perimeter of the shaded area is equal to (FIGURE) (a) 88 cm (b) 176 cm (c) 264 cm (d) 352 cm
View SolutionThe area of the shaded portion is (FIGURE) (a) 10 sq. cm (b) 14 sq. cm (c) 21 sq. cm (d) 25 sq. cm
View SolutionIn the figure, radius of the circle is 14 cm, then the shaded area is
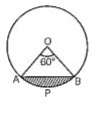
View SolutionIn the given figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O, then find the area of the shaded region.

View SolutionIn the given figure, PQ = 24 cm PR = 7 cm and O is the centre of the circle. Find the area of the shaded region. (Use π=3.14)

View SolutionIn Fig. 10.93, there are two concentric circles with centre O . PR and PQS are tangents to the inner circle from point plying on the outer circle. If PR=7.5cm , then PS is equal to (FIGURE) (a) 10cm (b) 12cm (c) 15cm (d) 18cm
View SolutionIn Fig. 10.87, two equal circles touch each other at T , if QP=4.5cm , then QR= (FIGURE) (a) 9cm (b) 18cm (c) 15cm (d) 13.5cm
View SolutionIn the given figure, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O, then the area of the shaded region is :
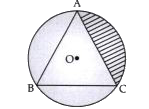
View SolutionIn Fig. 10.79, RQ is a tangent to the circle with centre O . If SQ=6cm and QR=4cm , then OR= (FIGURE) (a) 8cm (b) 3cm (c) 2.5cm (d) 5cm
View SolutionThe diameter of a circle is equal to the perimeter of a square whose area is 3136 cm2. What is the circumference of the circle? (a) 352 cm (b) 704 cm (c) 39424 cm (d) 1024 cm
View Solution
