If the surface area of a cube is 13254 cm2, then the length of its diagonal is 44√3cm (b) 45√3cm (c) 46√3cm (d) 47√3cm
To find the length of the diagonal of a cube given its surface area, we can follow these steps:
Step 1: Understand the formula for the surface area of a cube.
The surface area S of a cube is given by the formula:
S=6a2
where a is the length of one side of the cube.
Step 2: Set up the equation using the given surface area.
We are given that the surface area of the cube is 13254cm2. Therefore, we can set up the equation:
6a2=13254
Step 3: Solve for a2.
To find a2, we divide both sides of the equation by 6:
a2=132546
Calculating the right side:
a2=2209cm2
Step 4: Find a by taking the square root of a2.
Now, we take the square root of both sides to find a:
a=√2209
Calculating the square root:
a=47cm
Step 5: Calculate the length of the diagonal of the cube.
The length of the diagonal d of a cube can be calculated using the formula:
d=a√3
Substituting the value of a:
d=47√3cm
Conclusion
Thus, the length of the diagonal of the cube is:
d=47√3cm
Final Answer
The correct option is (d) 47√3cm.
---
The surface area S of a cube is given by the formula:
S=6a2
where a is the length of one side of the cube.
We are given that the surface area of the cube is 13254cm2. Therefore, we can set up the equation:
6a2=13254
To find a2, we divide both sides of the equation by 6:
a2=132546
Calculating the right side:
a2=2209cm2
Now, we take the square root of both sides to find a:
a=√2209
Calculating the square root:
a=47cm
The length of the diagonal d of a cube can be calculated using the formula:
d=a√3
Substituting the value of a:
d=47√3cm
Thus, the length of the diagonal of the cube is:
d=47√3cm
The correct option is (d) 47√3cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the length of the diagonal of a cube is 6√3 cm , then length of the edge of the cube is 3 cm .
A2 cmB3 cmC6 cmD36√3 cmIn the adjoining figure, the length of BC is
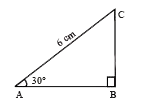
(a)2√3 cm
(b)3√3 cm
(c)4√3 cm
(d)3 cmA2√3 cmB3√3 cmC4√3 cmD3 cmIf the length of diagonal of a cube is 8√3cm then its surface area is
A192cm2B384cm2C512cm2D768cm2
ABCD is a square of side 4 cm. If E is a point in the interior of the square such that CED is equilateral, then area of ACE is (a) 2(√3−1)cm2 (b) 4(√3−1)cm2 (c) 6(√3−1)cm2 (d) 8(√3−1)cm2
View SolutionThe area of an equilateral triangle is 4√3 cm2. The length of each of its side is (a)3 cm (b) 4 cm (c)2√3 cm (d) √32 cm
View SolutionThe area of a square is twice that of a rectangle. The perimeter of the rectangle is 10 cm. If its length and breadth each is increased by 1 cm, the area of the rectangle becomes equal to the area of the square. The length of side of the square is 2√3cm (b) 3√2cm (c) 4√3cm (d) 12 cm
View SolutionIf the total length of diagonals of a cube is 12 cm, then what is the total length of the edges of the cube? 6√3cm (b) 12cm (c) 15cm (d) 12√3cm
View SolutionIf the length of diagonal of a cube is 8√3cm then its surface area is
View Solution
