From a cube of side 8m, a square hole of 3m side is hollowed from end to end. What is the volume of the remaining solid? (a) 440 m3 (b) 480 m3 (c) 508 m3 (d) 520 m3
To find the volume of the remaining solid after hollowing out a square hole from a cube, we can follow these steps:
Step 1: Calculate the volume of the original cube.
The formula for the volume V of a cube with side length a is given by:
V=a3
For our cube with a side length of 8 m:
V=83=512m3
Step 2: Calculate the volume of the hollowed-out square hole.
The hole is a rectangular prism with a square base of side length 3 m and a height equal to the side of the cube, which is 8 m. The volume Vh of the hole can be calculated using the formula:
Vh=base area×height
The base area of the square hole is:
base area=3×3=9m2
Thus, the volume of the hole is:
Vh=9×8=72m3
Step 3: Calculate the volume of the remaining solid.
To find the volume of the remaining solid, subtract the volume of the hole from the volume of the original cube:
Vremaining=V−Vh=512−72=440m3
Final Answer:
The volume of the remaining solid is 440m3. Therefore, the correct option is (a) 440 m³.
---
The formula for the volume V of a cube with side length a is given by:
V=a3
For our cube with a side length of 8 m:
V=83=512m3
The hole is a rectangular prism with a square base of side length 3 m and a height equal to the side of the cube, which is 8 m. The volume Vh of the hole can be calculated using the formula:
Vh=base area×height
The base area of the square hole is:
base area=3×3=9m2
Thus, the volume of the hole is:
Vh=9×8=72m3
To find the volume of the remaining solid, subtract the volume of the hole from the volume of the original cube:
Vremaining=V−Vh=512−72=440m3
The volume of the remaining solid is 440m3. Therefore, the correct option is (a) 440 m³.
Topper's Solved these Questions
Similar Questions
Knowledge Check
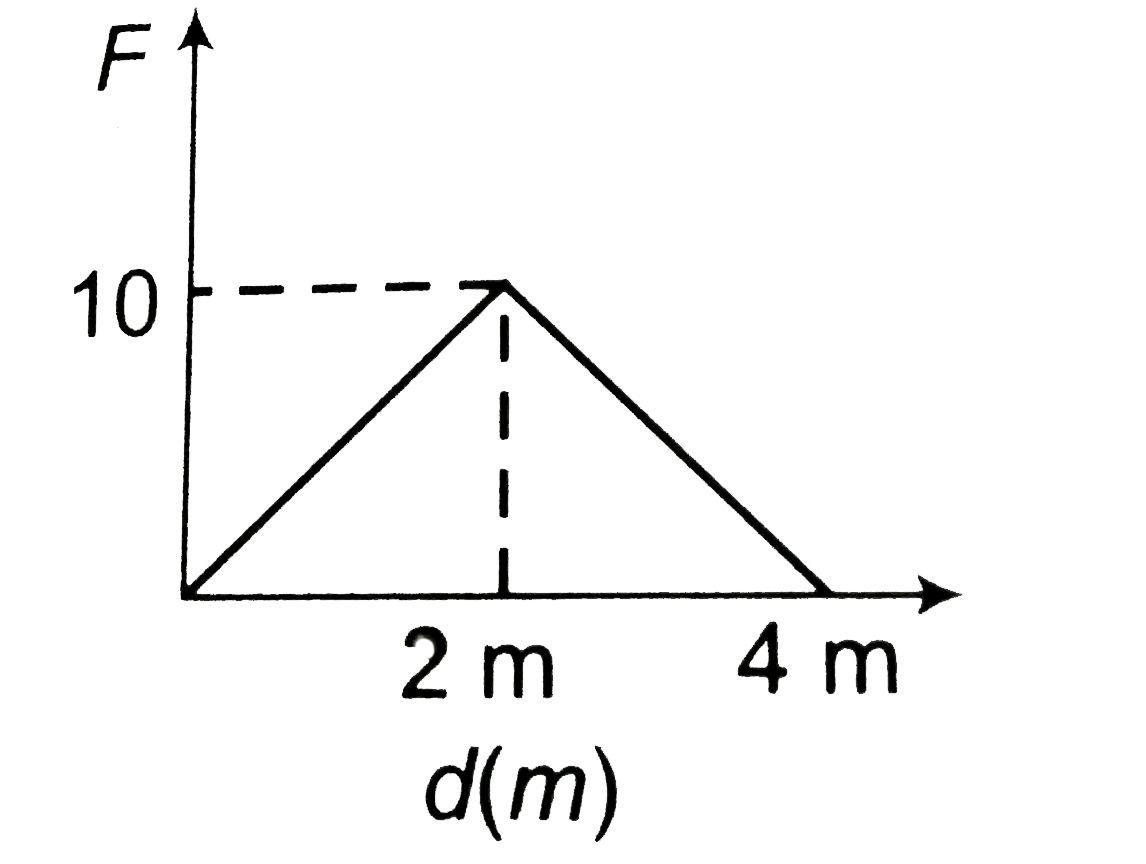
Work done from d=0m to d=3mA12.5 JB15 JC17.5 JD20 JThere is a solid cube with side 10 m. If the largest possible cone is carved out of it, then what is the surface area of the remaining part of the cube?
A600+25√5πB500+25√5πC600−25(√5+1πD600+25(√5−1)π
A right pyramid is on a regular hexagonal base. Each side of the base is 10 m and the height is 60 m. The volume of the pyramid is (a) 5000 m3 (b) 5100 m3 (c) 5195 m3 (d) 5196 m3
View SolutionTwo cubes each of volume 64 cm3 are joined end to end. Find the surface area and volume of the resulting cuboid.
View SolutionA circular well with a diameter of 2 metres, is dug to a depth of 14 metres. What is the volume of the earth dug out? (a) 32 m3 (b) 36 m3 (c) 40 m3 (d) 44 m3
View SolutionThe largest sphere is cut off from a cube of side 6cm. The volume of the sphere will be 27π cm3 (b) 36π cm3 (c) 108π cm3 (d) 12π cm3
View SolutionTwo cubes, each of volume 512 cm3 are joined end to end. Find the surface area of the resulting cuboid.
View SolutionThe base of a pyramid is an equilateral triangle of side 1 m. If the height of the pyramid is 4 metres, then the volume is (a) 0.550 m3 (b) 0.577 m3 (c) 0.678 m3 (d) 0.750 m3
View Solution
