Question

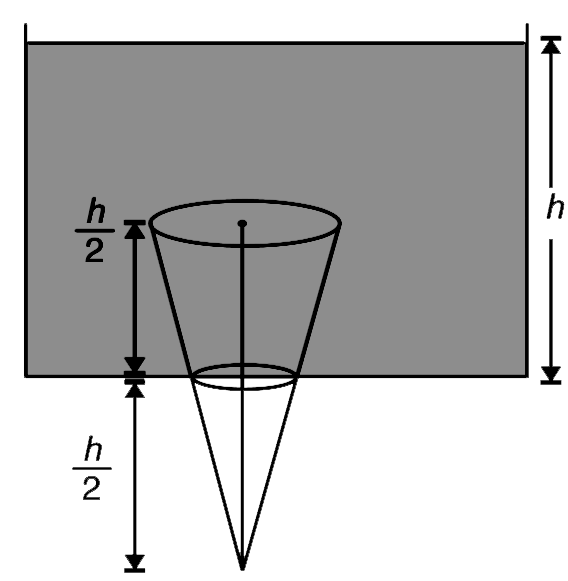
A vertical
cone of volume $V$
with vertex
downwards is filled with water upto half of its height. The volume of the
water is
$\frac{V}{2}$
(b) $\frac{V}{4}$
(c) $\frac{V}{8}$
(d) $\frac{V}{16}$

Explanation

To solve the problem of finding the volume of water in a vertical cone filled to half its height, we can follow these steps:

1. Understand the Volume of the Cone:
The volume \( V \) of a cone is given by the formula:
\( V = \frac{1}{3} \pi R^2 H \)
where \( R \) is the radius of the base and \( H \) is the height of the cone.

2. Identify the Height of Water:
The cone is filled with water up to half of its height. Therefore, the height of the water \( h \) is:
\( h = \frac{H}{2} \)

3. Determine the Radius of the Water Surface:
Since the cone is similar in shape when filled with water, we can use the properties of similar triangles to find the radius of the water surface \( r \) when the height is \( h \).
From the similarity of triangles:
\( \frac{R}{H} = \frac{r}{h} \)
Substituting \( h = \frac{H}{2} \):
\( \frac{R}{H} = \frac{r}{\frac{H}{2}} \)
This simplifies to:
\( r = \frac{R}{2} \)

4. Calculate the Volume of Water:
Now, we can find the volume of the water \( V_{water} \) using the radius \( r \) and height \( h \):
\( V_{water} = \frac{1}{3} \pi r^2 h \)
Substituting \( r = \frac{R}{2} \) and \( h = \frac{H}{2} \):
\( V_{water} = \frac{1}{3} \pi \left(\frac{R}{2}\right)^2 \left(\frac{H}{2}\right) \)
Simplifying this expression:
\( V_{water} = \frac{1}{3} \pi \frac{R^2}{4} \cdot \frac{H}{2} = \frac{1}{3} \cdot \frac{1}{4} \cdot \frac{1}{2} \pi R^2 H = \frac{1}{24} \pi R^2 H \)

5. Relate the Volume of Water to the Original Cone Volume:
Recall the original volume \( V = \frac{1}{3} \pi R^2 H \). Therefore:
\( V_{water} = \frac{1}{24} \pi R^2 H = \frac{1}{8} \cdot \frac{1}{3} \pi R^2 H = \frac{1}{8} V \)

6. Conclusion:
The volume of the water in the cone is:
\( V_{water} = \frac{V}{8} \)
Thus, the correct answer is option (c) \( \frac{V}{8} \).