A transport company has two main depots P and Q, from where buses are sent to three subdepots A,B and C in difference parts of a region. The number of buses available at P and Q are 12 and 18 . The requirements of A,B and C are 9, 13 and 8 buses respectively. The distance between the two main depots and the three sub-depots are given in the following table ( in km ).

How should the buses be sent from P and Q to A,B and C, so that the total distance covered by the buses is the minimum ?
Let x buses be sent from P to A, and y buses be sent from P to B.
Since , P has only 12 buses, so 12-(x+y) buses are sent from P to C.
Since, 9 buses are required for A , and x buses are sent from P, so (9-x) buses should be sent from Q to A . Similarly, the number of buses to be sent from Q to B is 13-y, and the number of buses to be sent from Q to C is 18-(9-x+13-y) or x+y-4.
The above can be represented in the following table :
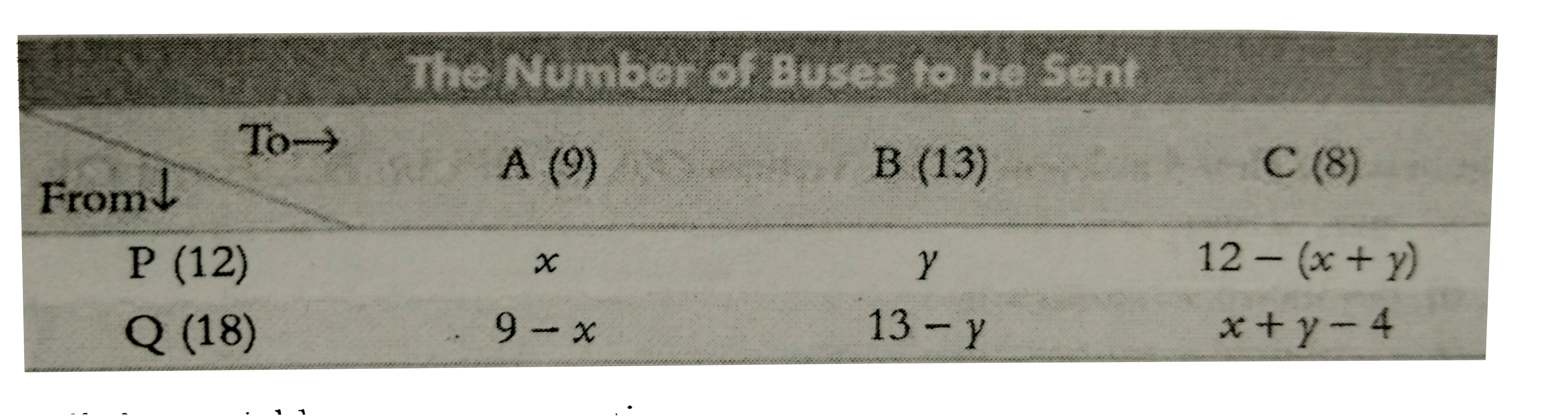
All the variables are non- negative.
The given condition are :
x≥0andx≤9
y≥0andy≤13
The region which satisfies the above set of inequalities is the rectangle OGBC.
The graph of x+y≥4 is shown with horizontal lines and the graph of x+y≤12 is shown with vertical lines.
∴ The feasible region is the area with both horizontal and vertical lines within the rectangular region OGBC , i.e., the polygonal region FGHDE.
The distance covered by the buses
d=15x+40y+50(12−(x+y))+20(9−x)+30(13−y)+70(x+y−4)
=15x+40y+600−50x50y+180−20x+390−30y+70x+70y−280
=15x+30y+890

∴ We have to minimize the distance d.
In the graph, DEFGH is a closed -convex polygon with vertices F(4,0), G(9,0), H(9,3), D(0,12) and E(0,4) objective function d=15x+30y+890.
At vertex F(4,0), d=15(4)+30(0)+890=60+890=950.
At vertex G(9,0), d=15(9)+30(0)+890=1025
At vertex H(9,3),d=15(9)+30(3)+890=1115
At vertex D(0,12),d=15(0)+30(12)+890=1250
At vertex E(0,4) , d=15(0)+30(4)+890=1010
∴ d is minimum at F(4,0)
∴ x=4,y=0
∴ 4 buses have to be sent from P to A, and 8 buses have to be sent from P to C. Also, 5 buses have to be sent from Q to A , and 13 buses have to be sent from Q to minimize the distance travelled.

Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Very short Answer Type questions
14 Videos
- LINEAR PROGRAMMINGBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - Short anwere Type Question
10 Videos
- LIMITSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIMITSEXERCISE - LEVEL-3
15 Videos
- LOGARITHMSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LOGARITHMSEXERCISE - Level 3
15 Videos
Similar Questions
An oil company has two depots, A and B, with capacities of 7000 L and 4000 L respectively. The company is to supply oil to three pumps D,E,F whose requirements are 4500 L, 3000 L and 3500 L respectively. The distance (in Km) between the depots and the petrol pumps are given in the following table :

Assuming that the transportation cost of10 litres of oil is ₹ 1 per km , how should the delivery be scheduled in order that the transportation cost is minimum ?
View SolutionAn oil company has two depots A and B with capacities of 7000 L and 4000 L respectively. The company is to supply oil to three petrol pumps, D, E and F whose requirements are 4500L, 3000L and 3500L respectively. The distances (in km) between the depots and the petrol pumps is given in the following table:
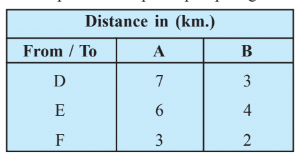
Assuming that the transportation cost of 10 litres of oil is Re 1 per km, how should the delivery be scheduled in order that the transportation cost is minimum? What is the minimum cost?
View Solution
Knowledge Check
Two buses are moving towards each other with speed of 20 km/hr and 34km/hr respectively. What will be the distance (in metres) between the two buses one second before they collide?
A21B18C12D15Three numbers a, b, c are lies between 2 and 18 such that their sum is 25. 2, a, b, are in A.P, and b, c, 18 are in G.P. Then abc =
A360B420C480D540
An oil company has two depots A and B with capacities of 7000L and 4000L respectively. The company is to supply oil to three petrol pumps, D,E and F whose requirements are 4500L,3000L and 3500L respectively. The distances (in km) between the depots and the petrol pumpa is given in the following table:

Assuming that the transportation cost of 10 litres of oil is Rs. 1 per km, how shold the delivery be scheduled in order that the transportation cost is minimum? What is the minimum cost?
View SolutionLet AB and CD are two parallel chords of circle whose radius is 5 units. If P and Q are mid points of AB and CD respectively such that PA.PB=9,QC.QD=16, then distance betweẹn AB and CD is
View SolutionTwo stations A and B are 500 km away. If two buses each start from station A and B simultaneously travelling towards the other station with speeds 80 km/h and 90 km/h , respectively, find the distance between the two buses exactly after 2 h.
View SolutionThere are two factories located one at place P and the other at place Q.From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirments of the depots are respectively 5,5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below:
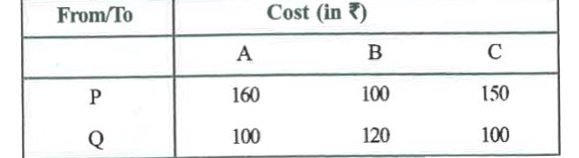
How many units should be transported from each factory to each depot in order that the transportable cost is minimum? When will be the minimum transportation cost?
View SolutionThere are factories located one at place P and other at place Q from which a certin commodity is to be delivered to each of three depot situated at A,B and C. The weekly requirement of the depots are respectively 5,5 and 4 units of the commodity while the production capacity of the factories P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below.
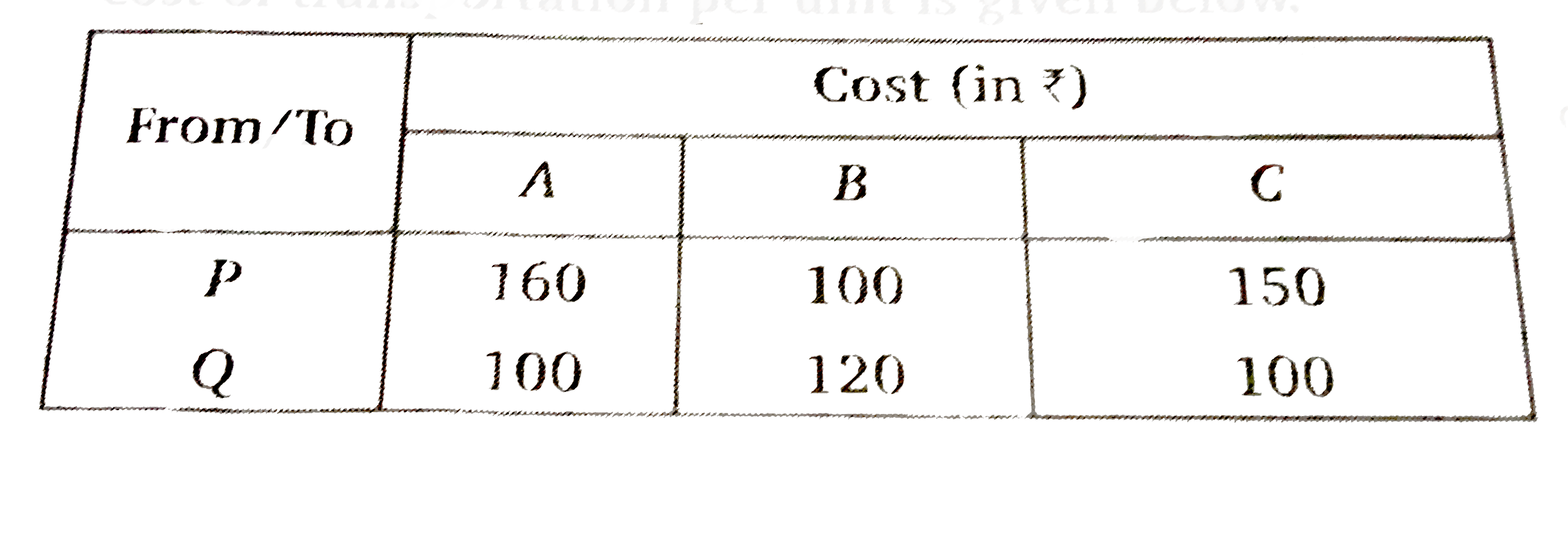
How many units should be transported from each factory to each depot in order that the transportation cost is minimum. Also find the minimum transportation cost.
View SolutionThe speeds of three buses are in the ratio 2:3: 4. The time taken by these buses to travel the same distance will be in the ratio
View Solution
