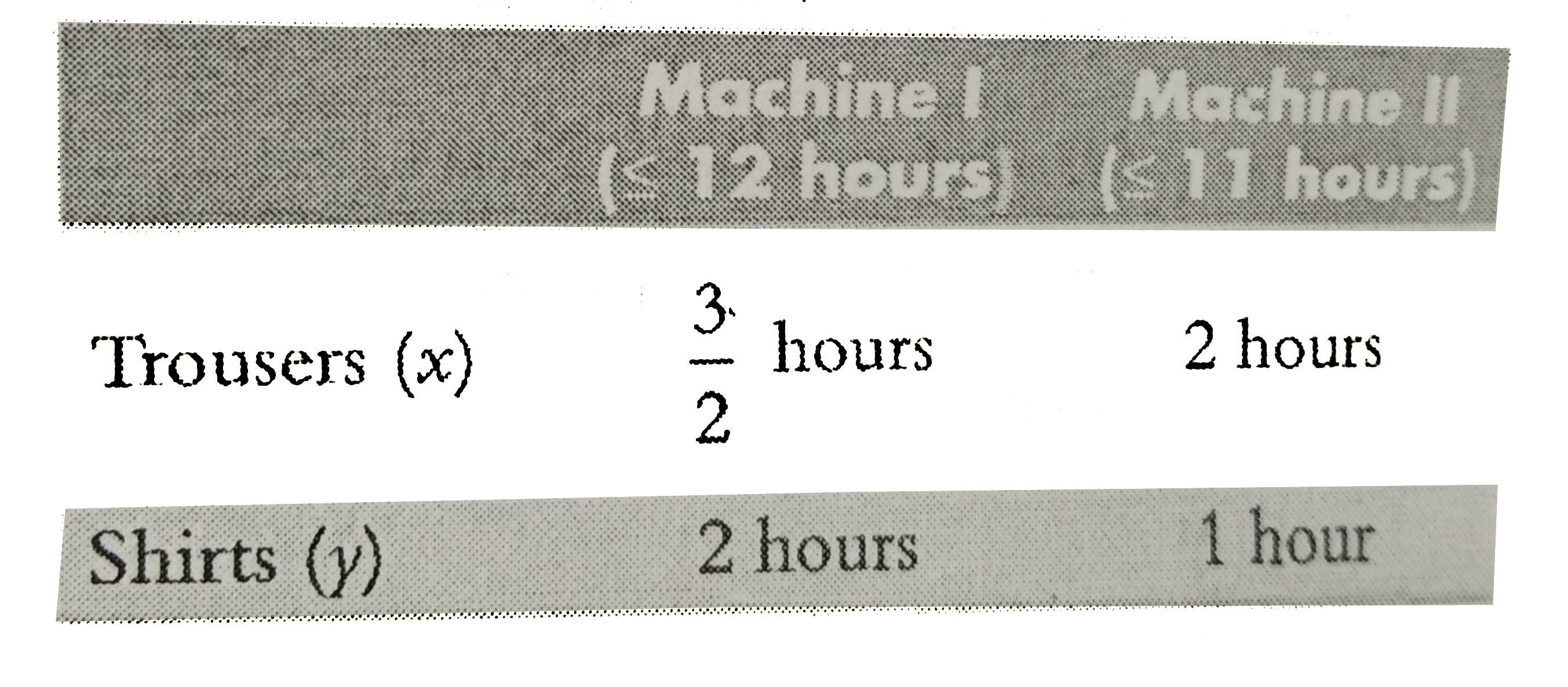
A tailor stiches trousers and shirts and each piece is completed by two machine I and II. To complete each trousers, machines I and II must work 3/2 hours and 2 hours respectively, and to complete each shirt, machines I and II must work 2 hours and 1 hours respectively Machine I may not operate for more than 12 hours ped day and machine II not more than 11 hours per day. If the profit on each trouser and each shirt is Rs. 150 and Rs. 100 repectively, then the maximum profit is _______
Rs. 900
Rs. 500
Rs. 375
Rs. 600
The correct Answer is:A
Let the number of trousers =x
Let the number of shirts=y
According to the given condition :
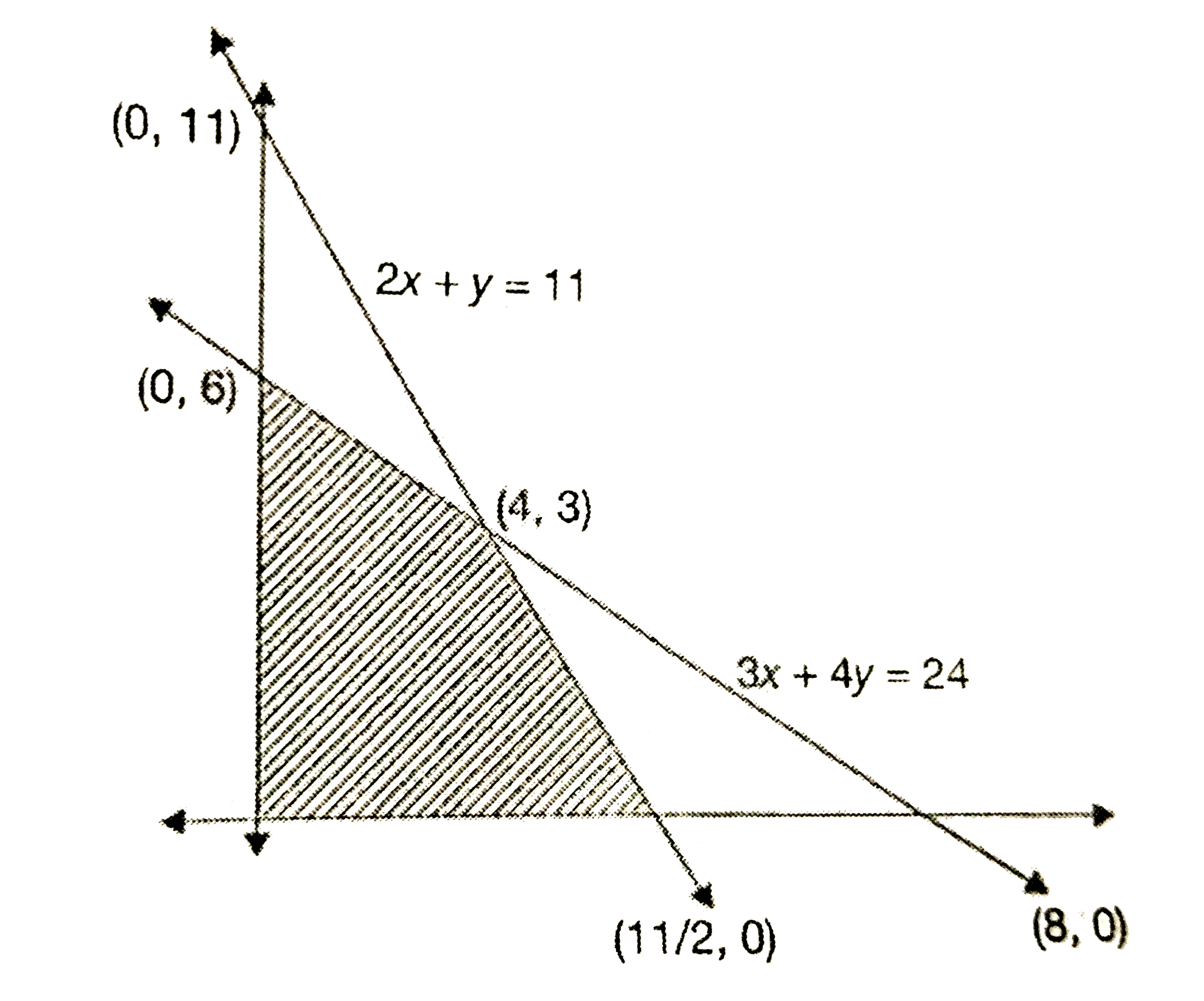
⇒3x2+2y≤12and2x+y≤11
⇒3x+4y≤24and2x+y≤11
x≥0,y≥0
The profit function , p=15x+10y
The shaded region is a closed- convex polygon with vertices (112,0),(4,3),(0,6),(0,0).
∴ ABCD is the feasible reason.
∴ THe maximum profit is at C(4,3), i.e.,
P=150×4+100×3=900.
Topper's Solved these Questions
Similar Questions
A manufacturer makes two models A and B of a product. Each model is processed by two machines. To complete one unit of model. A, machines I and II must work 1 hours and 3 hours respectively. To complete one unit of model B, machine I and II must work 2 hours and 1 hour respectively. Machine I may not operate for more than 8 hours per day, and machine II for not more than 9 hours per day. If profits on model A and B per unit are Rs. 300 and Rs. 350, then how many units of each model should be produced , per day, to maximize the profits ?
View SolutionA factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftmans time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftmans time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsmans time. If the profit on a racket and on a bat is Rs. 20 and Rs. 10 respectively, find the number of tennis rackets and crickets bats that the factory must manufacture to earn the maximum profit. Make it as an L.P.P. and solve graphically.
View SolutionA factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftmans time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftmans time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsmans time. If the profit on a racket and on a bat is Rs. 20 and Rs. 10 respectively, find the number of tennis rackets and crickets bats that the factory must manufacture to earn the maximum profit. Make it as an L.P.P. and solve graphically.
View SolutionA factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftmans time m its making while a cricket bat takes 3 hour of machine time and 1 hour of craftmans time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsmans time.(i) What number of rackets and bats must be made if the factory is to work at full capacity?(ii) If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the maximum profit of the factory when it works at full capacity.
View SolutionA factory makes tennis rackets and cricket bats. A tennis rackets takes 1.5 hour of machine time and 3 hours of craftman's time in its making while a cricket bat takes 3 hour of machine time and 1 hour of cratman's time. In a daythe factory has the availability of not more than 42 hours of machine time and 24 hours of craftman's time.
(i) What number of rackets and bats must be made if the factory is to work at full capacity?
(ii) If profit on a racket and on a bat is Rs. 20 and Rs. 10 respectively, find the maximum profit of the factory when it works at full capacity.
View SolutionMachine X can pack 30 articles per hour and machine Y can pack 35 articles per hour. MachineX works for x hours per day and machine Y works for y hours per day and both the machinespack at least 2500 articles in a day. Frame an inequation to represent the above data.
View SolutionMachine X can pack 30 articles per hour and machine Y can pack 35 articles per hour. Machine X works for x hours per day and machine Y works for y hours per day and both the machines pack at least 2500 articles in a day. Frame and inequation to represent the above data.
View SolutionA toy manufacturing farm produces toys T1andT2 each of which must be processed through two machines M1andM2. The maximum availablity of machines M1andM2 per day are 14 hours and 20 hours respectively. Manufacturing of toy T1, requires 5 hours on machine M1 If the 3 hours on machine M2 whereas toy T2, requires 4 hours on machine M1, and 6 hours on machine M2. If the profit on manufacturing of toy T, is Rs.50 and profit on manufacturing of toy T2 is Rs.70, formulate this problem as L.P.P. in order to maximize the profit.
View SolutionA manufacture produceds two types of steel trunks. He has two machines, A and B. The first type of book case requires 3 hours on machine A and 3 hours on machine B for completion whereas the second type required 3 hours on machine A and 2 hours n machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs.30 and Rs.25 per trunk of the first type and second type respectively. How many trunks of each type must he make each day to make the maximum profit?
View SolutionA manufacturer produces two types of steel trunks. He has tow machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs. 30 and Rs. 25 per trunk of the first type and the second respectively. How many trunks of each type must he make each day to makes maximum profit?
View Solution
