Doubtnut Promotions Sticky

Let the quadratic equation (c−5)x2−2cx+c−4=0 has one root in (0,2) and other root in (2,3) then find the number of intergral values of c in solution set (a) 18 (b) 12 (c) 11 (d) 10

A

11

B

10

C

12

D

18

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Let f(x)=(c−5)x2−2cx+(c−4)=0.
Then, according to problem, the graph of g=f(x) will be either of the two ways, show below.
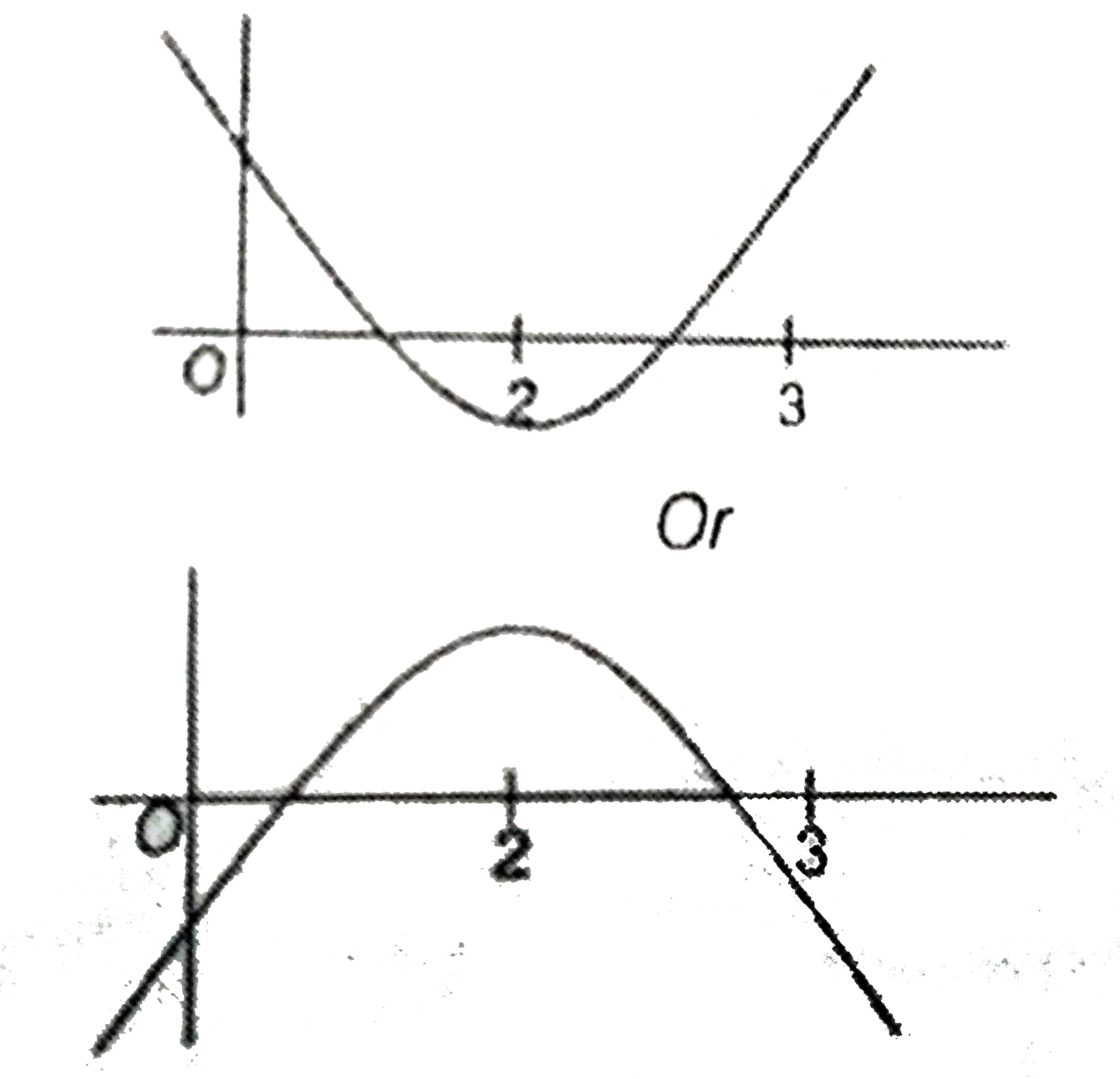
ocr_image
In both cases f(0).f(2)<0andf(2)f(3)<0
Now, consider f(0)f92)<0
⇒(c−4)[4(c−5)−4c+(c−4)]<0
⇒(c−4)(c−24)<0
⇒c∈(4,24) ...(i)
ocr_image
Similiarly, f(2).f(3)<0
⇒[4(c−5)−4c+(c−4)]
[9(c−5)−6c+(c−4)]<0
⇒(c−24)(4c−49)<0
ocr_image
⇒c∈(494,24) ...(ii)
From Eqs. (i) and (ii), we get
c∈(494,24)
∴ Integral vaues of c are 13,14 ....., 23, Thus, 11 integral values of c are possible.

|
Updated on:21/07/2023
Class 12MATHSQUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    The roots of the equation
    (a+c−b)x2−2cx+(b+c−a)=0 are

    A1,2ca+c−b
    B1,b+c−aa+c−b
    C1,b+c−a2c
    D1,a+c−bb+c−a
  • Question 2 - Select One

    If the roots of 10x3−cx2−54x−270 are in harmonic progression, then find c and all the roots.

    A2
    B6
    C9
    Dnone of these
  • Question 3 - Select One

    If the quadratic equations, ax2+2cx+b=0andax2+2bx+c=0(b≠c) have a common root, then a+4b+4c is equal to: a. -2 b. -2 c. 0 d. 1

    A−2
    B−1
    C0
    D1