If the roots of the equation x2−2ax+a2−a−3=0 are ra and less than 3, then a<2 b. 2<−a≤3 c. 3<a≤4 d. a>4
a<2
2≤a≤3
3<a≤4
a>4
The correct Answer is:A
Let f(x)=x2−2ax+a2+a−3
Since, both root are less than 3.
⇒a<3,β<3
⇒Sum,S=α+β<6
⇒α+β2<3
⇒2a2<3
⇒a<3 ...(i)
Again, product, P=αβ
⇒P<9⇒αβ<9
⇒a2+a−3<9
⇒a2+a−12<0
⇒(a−3)(a+4)<0
⇒−4<a<2 ..(ii)
Again, D=B2−4AC≥0
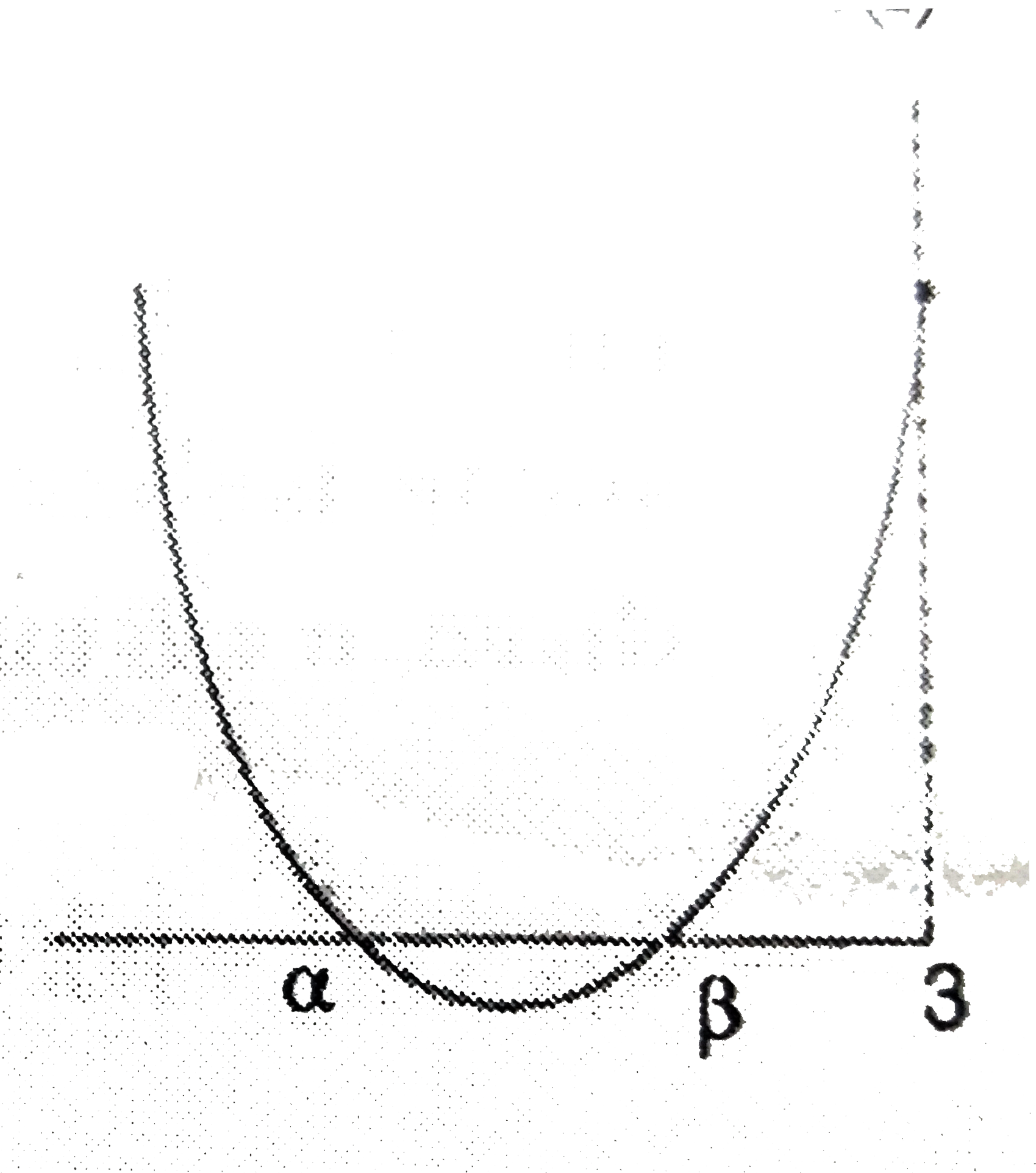
⇒(−2a)2−4.1(a2+a−3)≥0
⇒4a2−4a2−4a+12≥0
⇒−4a+12≥0⇒a≤3 ...(iii)
Again, = af(3)>0
⇒1.[(3)2−2a(3)+a2+a−3]>0
⇒9−6a+a2+a−3>0
⇒a2−5a+6>0
⇒(a−2)(a−3)>0
∴a∈(−∞,2)∪?(2,∞) ...(iv)
From Eqs. (i),(ii),(iii), and (iv), we get a∈(−4,2).
Note There is correction in answer <2should be−4<a<2.
Topper's Solved these Questions
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - THEORY OF EQUATIONSEXERCISE - SOME SPECIAL FORMS18videos
THEORY OF EQUATIONS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - THEORY OF EQUATIONSEXERCISE - TRANFRORMATION OF ROOTS2videos
THEORY OF EQUATIONS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - STRAIGHT LINE AND PAIR OF STRAIGHT LINESEXERCISE - GENERAL EQUATION OF PAIR OF STRAIGHT LINES (Objective Questions I) (Only one correct option)1videos
STRAIGHT LINE AND PAIR OF STRAIGHT LINES
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - TRIGONOMETRICAL EQUATIONSEXERCISE - TOPIC 3 PROBLEMS BASED ON MAXIMUM AND MINIMUM OBJECTEIVE QUESTIONS I (ONLY ONE CORRECT OPTION)9videos
TRIGONOMETRICAL EQUATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
If the roots of the equation x2−2ax+a2+a−3=0 are real and less than 3, then
Aa<2B2≤a≤3C3<a≤4Da>4 - Question 2 - Select One
If the roots of the equation x2−2ax+a2+a
-3=0 are real and less than 3, then which
one of the following is correct ?Aa<2B2≤a≤3C3≤a≤4Da>4 - Question 3 - Select One
If the roots of the equation x2−2ax+a2+a−3=0are real and less than 3, then :
Aa<2B2≤a≤3C3<a≤4Da>4
If the roots of the equation x2−4ax+4a2+2a−3=0 are real and less than 3, then
View SolutionIf roots of the equation x2−2ax+a2+a−3=0 are real and less than 3 then a)a<2 b)2≤a≤3 c) 3l3a≤4 d)a>4
View SolutionMatch the following
Column-I Column -II(A) if the roots of the equationx2−2ax+a2+a−3=0 are real and less than 3, then a belongs to (p) a does not exist(B) If the roots of the equation x2−2ax+a2+a−3=0 are real and greater than , 3 then a belongs to (q) (32,3)(C) If exactly one root of the above equation lies in the interval (1,3) then a belongs to (r) (−1,2)∪(2,3)(D) IF the roots of the above equation are such that one root is greater than 3 and other smaller than 1, then a belongs to (s) (−∞,2)View SolutionFind the set of all values of a for which the roots of the equation x2−2ax+a2+a−3=0 are less than 3,
View SolutionIf the roots of the equation x2−2ax+a2+a−3=0are real and less than 3, then :
View Solution

