A tangent to the ellipse distance distance from the centre of the ellipse $x^{2} + 2 y^{2} = 6$ P and Q prove that the tangent at P and Q of the ellipse $x^{2} + 2 y^{2} = 6$ are at right angles .

Text Solution

Verified by Experts

given , $x^{2} + 4 y^{2} = 4 or \frac{x^{2}}{4} + \frac{y^{2}}{1} = 1$
Equation of any tangent to the ellipse on(i) can be written as
$\frac{x}{2} cos θ + y sin θ = 1$
Equation of second ellipse is

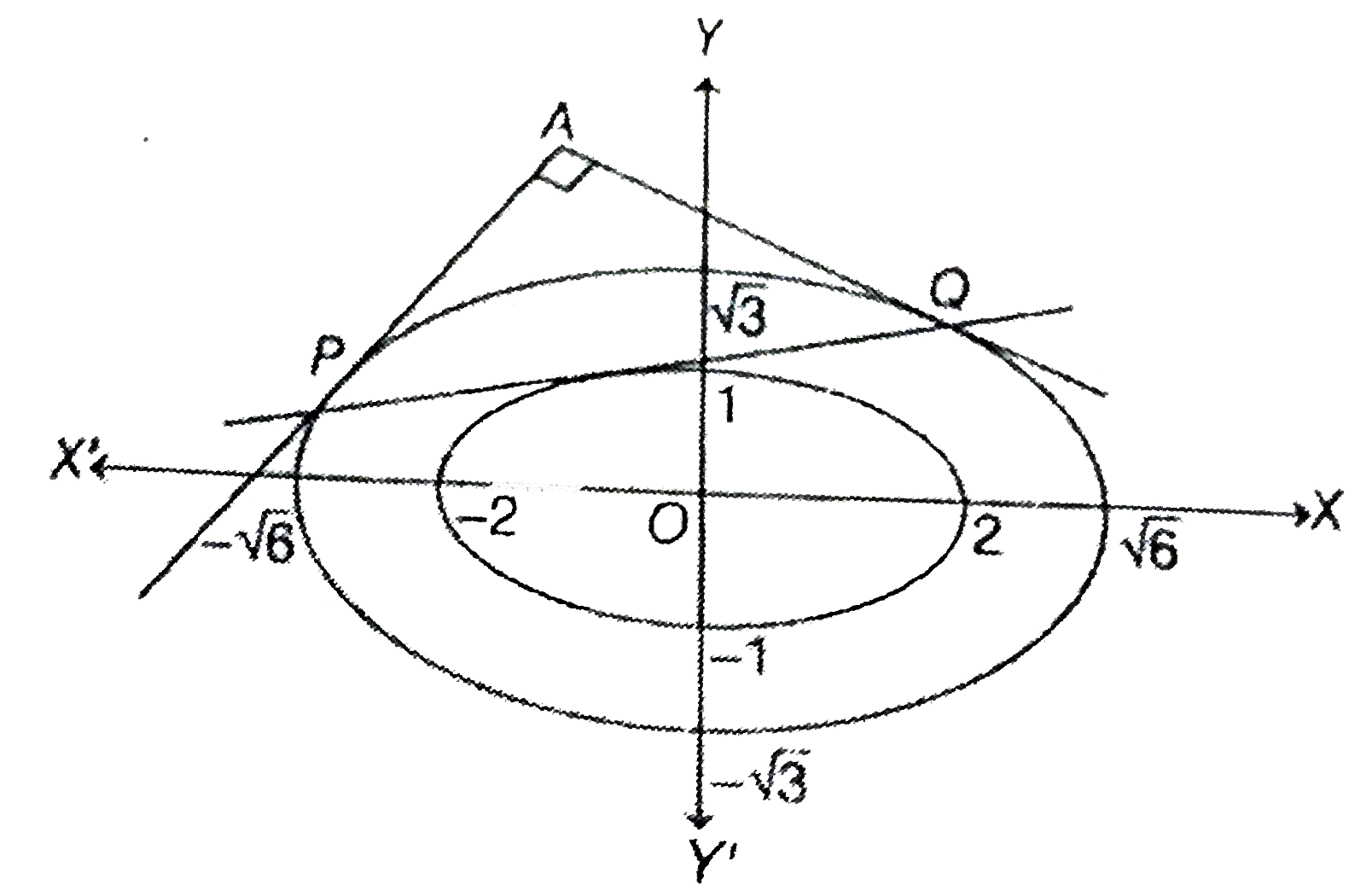
$x^{2} + 2 y^{2} = 6$
$\Rightarrow \frac{x^{2}}{6} + \frac{y^{2}}{3} = 1$
Suppose the tangent at P and Q meets at (h,k) Equation of the chord of contact of the tangents through A (h,k) is
$\frac{h x}{6} + \frac{k y}{3} = 1$
But Eqs . (iv) and (ii) represent the same straight line , so comparing Eqs. (iv) adn (ii) we get
$\frac{h / 6}{cos θ / 2} = \frac{k / 3}{sin θ} = \frac{1}{1}$
$\Rightarrow h = 3 cos θ and k = 3 sin θ$
therefore , coordinates of A are ( 3 cos, $θ, 3 sin θ)$
Now , the joint equation of the tangents At A is given by $T^{2} = S S_{1}$ ,
$i . e ., {(\frac{h x}{6} + \frac{k y}{3} - 1)}^{2} = (\frac{x^{2}}{6} + \frac{y^{2}}{3} - 1) (\frac{h^{2}}{6} + \frac{h^{2}}{3} - 1)$
in Eq. (v) Coefficient of $x^{2} = \frac{h^{2}}{36} - \frac{1}{6} (\frac{h^{2}}{6} + \frac{h^{2}}{3} - 1))$
$= \frac{h^{2}}{36} - \frac{h^{2}}{36} - \frac{k^{2}}{18} + \frac{1}{6} = \frac{1}{6} - \frac{k^{2}}{18}$
and coefficient of $y^{2} = \frac{k^{2}}{9} - \frac{1}{3} (\frac{h^{2}}{6} + \frac{k^{2}}{3} - 1)$
$= \frac{k^{2}}{9} - \frac{h^{2}}{18} - \frac{k^{2}}{9} + \frac{1}{3} = - \frac{h^{2}}{18 + \frac{1}{3}}$
Again , coefficient of $x^{2} +$ coefficient of $y^{2}$
$= - \frac{1}{18} (h^{2} + k^{2}) + \frac{1}{6} + \frac{1}{3}$
$= - \frac{1}{18} (9 {cos}^{2} θ + 9 {sin}^{2} θ + \frac{1}{2}$
$= - \frac{9}{18} + \frac{1}{2} = 0$
which shows that two lines represent by Eq. (v) are at right angles to each other .

Updated on:21/07/2023