The angle of elevation of the top of a vertical tower standing on a horizontal plane is observed to be 45∘ from a point A on the plane. Let B be the point 30 m vertically above the point A. If the angle of elevation of the top of the tower from B be 30∘, then the distance then the distance (in m) of the foot of the tower from the point A is
15(3+√3)
15(5−√3)
15(3−√3)
15(1+√3)
The correct Answer is:A
According to the question, we have the following figure.
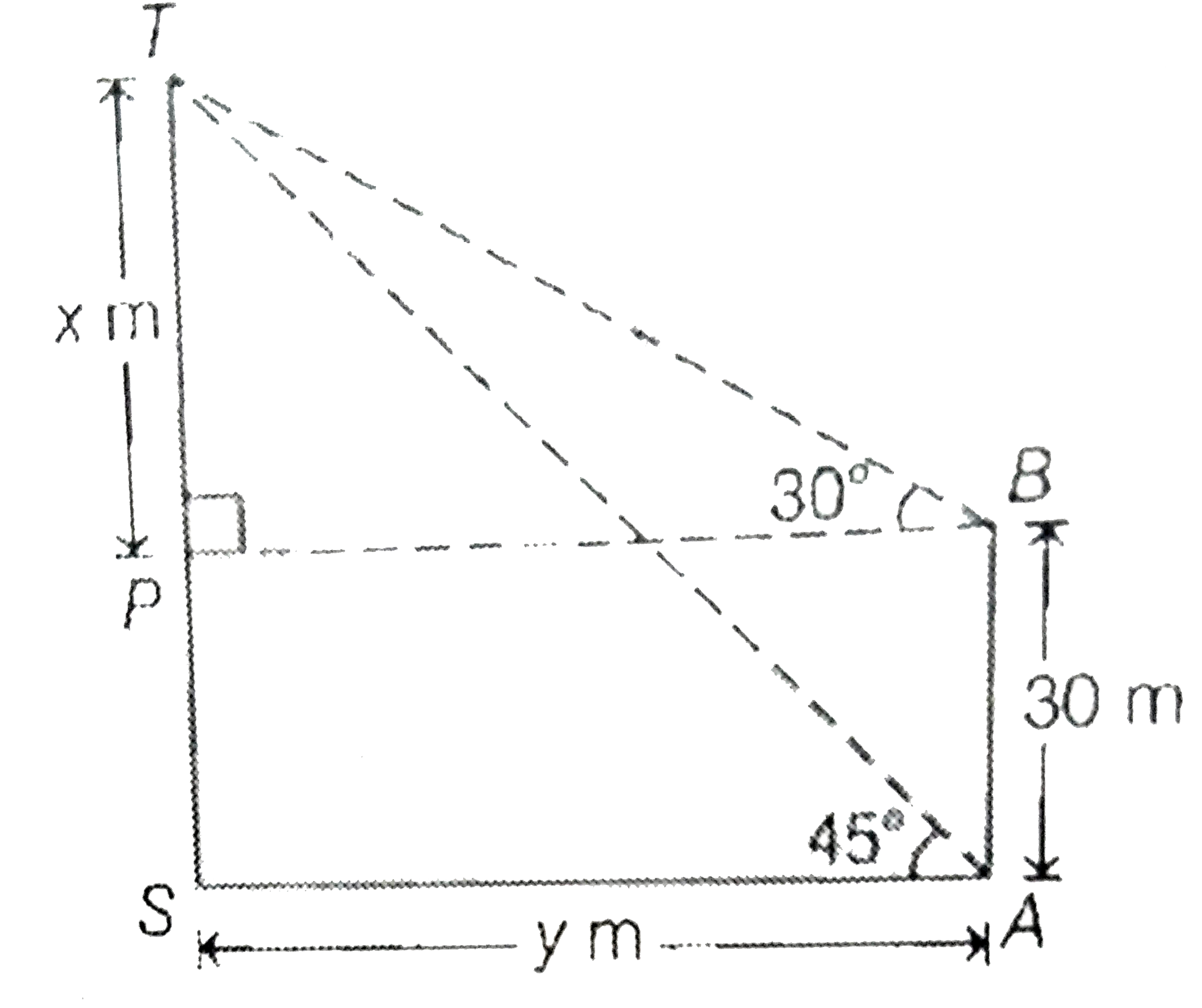
Now, let distance of foot of the tower from the point A is y m.
Draw BP⊥ST such that PT - x m.
Then, in ΔTPB, we have
tan30∘=xy
⇒x=1√3y ...(i)
and in ΔTSA, we have tan45∘=x+30y
⇒y=x+30 ...(ii)
On the elimination of quantity x from Eqs. (i) and (ii), we get
y=1√3y+30
⇒y(1−1√3=30)
⇒y=30√3√3−1=30√3(√3+1)3−1
=302√3(√3+1)=15(3+√3)
Topper's Solved these Questions
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - TRIGONOMETRICAL RATIOS AND IDENTITIESEXERCISE - MAXIMA AND MINIMA4videos
TRIGONOMETRICAL RATIOS AND IDENTITIES
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - TRIGONOMETRICAL EQUATIONSEXERCISE - TOPIC 3 PROBLEMS BASED ON MAXIMUM AND MINIMUM OBJECTEIVE QUESTIONS I (ONLY ONE CORRECT OPTION)9videos
TRIGONOMETRICAL EQUATIONS
- BOOK - IIT JEE PREVIOUS YEARCHAPTER - VECTOR ALGEBRAEXERCISE - Solving Equations and Reciprocal of Vectors (Objective Questions II) (Analytical & Descriptive Questions8videos
VECTOR ALGEBRA
Similar Questions
The angle of elevation of the top of a tower from a point on the ground, which is 25 m away from the foot of between the ship and tower.
View SolutionA tower of height 15 m stands vertically on the ground. From a point on the ground the angle of elevation of the top of the tower is found to be 30∘. What is the distance of the point from the foot of the tower?
View Solution
Knowledge Check
- Question 1 - Select One
The angle of elevation of the loop of a vertical tower standing on a horizontal plane is observed to be 45∘ from a point A on the plane. Let B be the point 30m vertically above the point A. If the angle of elevation of the top of the tower from B be 30∘, then the distance (in m) of the foot of the lower from the point A is:
A15(3+√3)B15(5−√3)C15(3−√3)D15(1+√3) - Question 2 - Select One
The angle of elevation of the top of a vertical tower situated perpendicularly on a plane is observed as 60∘ from a point P on the same plane .From another point Q , 10 m vertically above the point P , the angle of depression of the foot of the tower is 30∘ The height of the tower is
A15 mB30 mC20 mD25 m - Question 3 - Select One
At a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ The height of the tower is
A20√3mB20√3mC√320mDNone of these
The angle of elevation of the top of a tower of height 100√3m from a point at a distance of 100 m from the foot of the tower on a horizontal plane is
View SolutionFrom a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ . The height of the tower is
View SolutionAt a point 20 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ The height of the tower is
View SolutionA lower of height 15 m stands vertically on the ground. From a point on the ground the angle of elevation of the top of the tower is found to be 30∘. What is the distance of the point from the foot of the tower?
View SolutionThe angle of elevation of the top of a tower of height 100√3m from a point at a distance of 100 m from the foot of the tower on a horizontal plane is
View Solution

