Let a vertical tower AB have its end A on the level ground. Let C be the mid-point of AB and P be a point on the ground such that AP = 2AB. If √BPC=β, then tan β is equal to
67
14
29
49
The correct Answer is:C
Let AB = h, then AP = 2h
and AC = B C = h2
Again, let ∠CPA=α
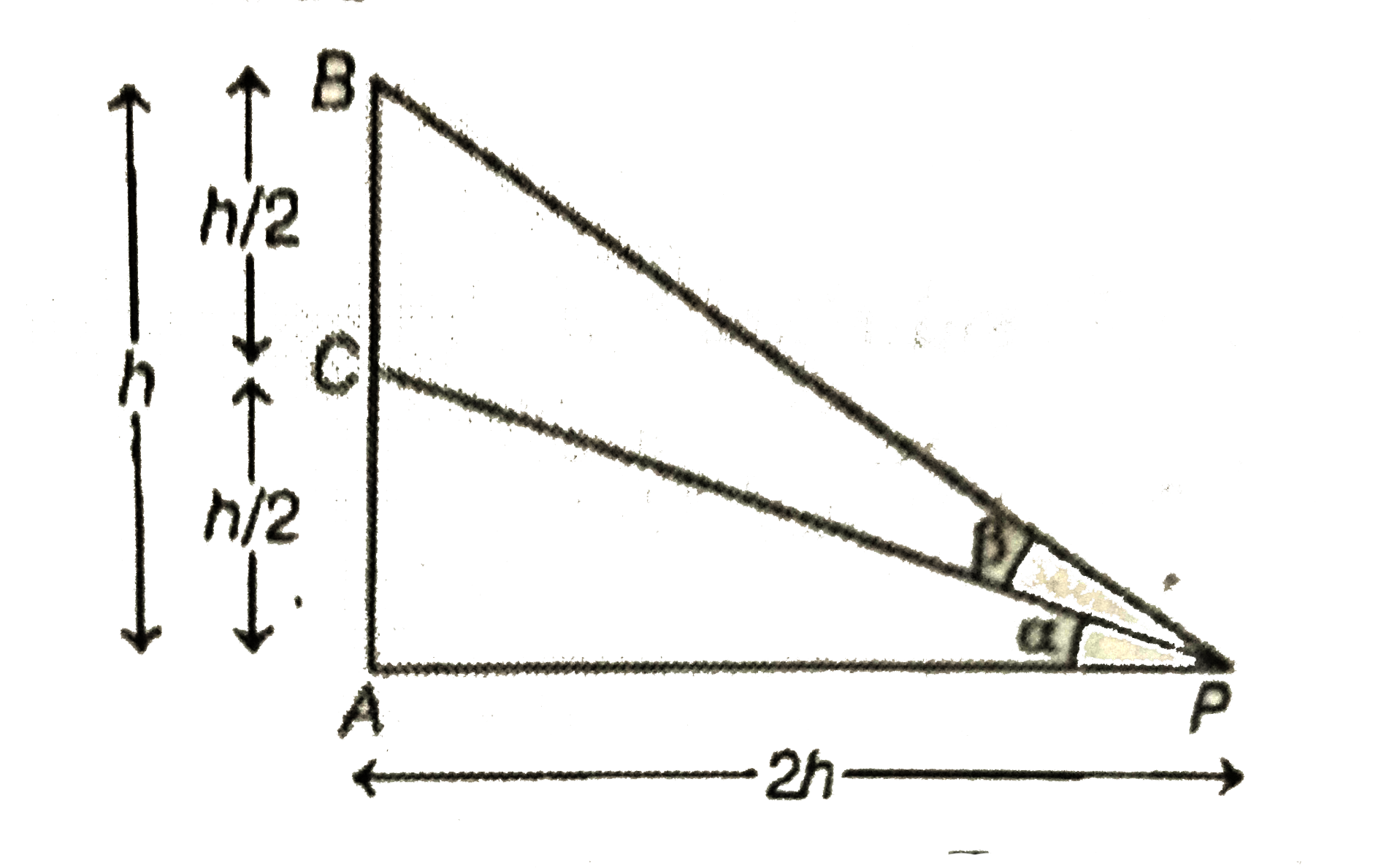
Now, in ∠ABP,tan(α+β)=ABAP=h2h=12
Also, in ΔACP,tanα=ACAP=22h=14
Now, tanβ=tan[(α+β)−α]
=tan(α+β)−tanα1+tan(α+β)tanα=12−141+12×14=1498=29
Topper's Solved these Questions
- TRIGONOMETRICAL RATIOS AND IDENTITIESBook:IIT JEE PREVIOUS YEARChapter:TRIGONOMETRICAL RATIOS AND IDENTITIESExercise:MAXIMA AND MINIMA
Explore 4 Videos
- TRIGONOMETRICAL EQUATIONSBook:IIT JEE PREVIOUS YEARChapter:TRIGONOMETRICAL EQUATIONSExercise:TOPIC 3 PROBLEMS BASED ON MAXIMUM AND MINIMUM OBJECTEIVE QUESTIONS I (ONLY ONE CORRECT OPTION)
Explore 9 Videos
- VECTOR ALGEBRABook:IIT JEE PREVIOUS YEARChapter:VECTOR ALGEBRAExercise:Solving Equations and Reciprocal of Vectors (Objective Questions II) (Analytical & Descriptive Questions
Explore 8 Videos
Similar Questions
Let a vertical tower Ab have its end A on the level ground. Let C be the mid point of AB and P be a point on the ground such that AP=2AB. If ∠BPC=β, then tanβ is equal to : 29 (2) 49 (3) 67 (4) 14
View SolutionLet a vertical tower AB have its end A on the level ground. Let C be the mid-point of AB and P be a point on the ground such that AP-2AB. If BPC-β, then tan β is equal to 12. 6 (2) 4 2 4
View Solution
Knowledge Check
If C is the mid-point of AB and P is any point outside AB, then
APA + PB = PCBPA + PB + 2 PC = 0CPA + PB - 2PC = 0DPA + PB + PC = 0If C is the mid-point of AB and P is any point outside AB, then
APA+PB+PC=0BPA+PB+2PC=0CPA+PB=PCDPA+PB=2PCIf C is the middle point of AB and P is any point outside AB, then
AP→A+P→B=P→CBP→A+P→B=2P→CCP→A+P→B+P→C=→0DP→A+P→B+2P→C=→0
If C is the middle point of AB and P is any point outside AB, then
View SolutionAB is a vertical pole. The end A is on the level ground .C is the middle point of AB. P is a point on the level ground . The portion BC subtends an angles β at P. If AP = nAB, then tan β=
View SolutionLet D be the mid-point of a straight line AB and let C be a point different from D such that AC=BC, then.
View SolutionLet D be the mid-point of a straight line AB and let C be a point different from D such that AC=BC, then.
View SolutionAB is a vertical pole. The end A is on the level ground .C is the middle point of AB. P is a point on the level ground . The portion BC subtends an angles β at P. If AP = nAB, then tan β=
View Solution
