కింది బాహుపదులకు (x+1) కరణాంకామగునో లేదో నిర్దారించండి. x4+2x3+2x2+x+1
Step by step video & image solution for కింది బాహుపదులకు (x+1) కరణాంకామగునో లేదో నిర్దారించండి. x^(4)+2x^(3)+2x^(2)+x+1 by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- బహుపదులు మరియు కరణాంకా విభజనBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - బహుపదులు మరియు కరణాంకా విభజనEXERCISE - Exapmle
15 Videos
- బహుపదులు మరియు కరణాంకా విభజనBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - బహుపదులు మరియు కరణాంకా విభజనEXERCISE - Exapmle
15 Videos
- నిరూపక జ్యామితిBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - నిరూపక జ్యామితిEXERCISE - Exercise
87 Videos
- రెండు చరరాశులలో రేఖీయ సమీకరణాలుBOOK - VGS PUBLICATION-BRILLIANT(TELUGU)CHAPTER - రెండు చరరాశులలో రేఖీయ సమీకరణాలుEXERCISE - Exercise
180 Videos
Similar Questions
కింద ఇవ్వబడిన బాహుపదులలో సూచించిన చరరాశి విలువను ప్రతిక్షేపించి విలువలు కనుగొనండి. X=1 వద్ద p(x)=4x2−3x+7
View Solutionకింద ఇవ్వబడిన బాహుపదులలో సూచించిన చరరాశి విలువను ప్రతిక్షేపించి విలువలు కనుగొనండి. X=1 వద్ద p(x)=4x2−3x+7
View Solutionఒక ఆవాస ప్రాంతంలో ప్రధాన రహదారి ఉత్తర-దక్షిణ దిశలలో ఉంది. దాని పటం కింది ఇవ్వబడినది. పటం సహాయంతో కింది ప్రశ్నలకు సమాధానాలు వ్రాయండి.
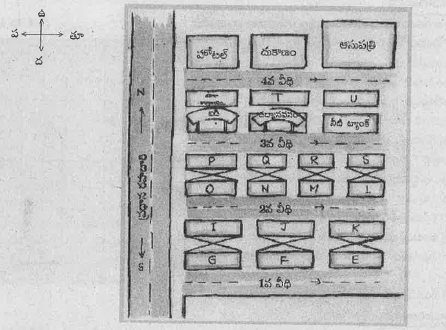తూర్పుదిక్కున వెళ్లునప్పుడు మూడవవీధిలో ఎడమవైపు మూడోవస్థానంలో ఏం ఉంది?
View Solutionకింది రేఖాసమీకరణలను ax+by+c=0 రూపంలో రాసి, ప్రతి సందర్భంలోను a,b మరియు c విలవును రాయండి. 3x+2y=9
View Solution∫x2−1x3√2x4−2x2+1dxisequa<o √2x4−2x2+1x3+C (b) √2x4−2x2+1x+C √2x4−2x2+1x2+C (d) √2x4−2x2+12x2+C
View SolutionEvaluate: ∫322x5+x4−2x3+2x2+1(x2+1)(x4−1)dx
View SolutionSimplify: (x3−2x2+3x−4)(x−1)− (2x−3)(x2−x+1)
View Solution(2x + 3) / (2x + 5)-(x) / (x + 1) = (1) / (2x + 3), (x! = -1, x! =-(5) / (2) , x! =-(3) / (2))
View Solutionसमीकरण (x2x+1)2+4(x2x+1)+3=0,(x≠−12) को हल कीजिए।
View Solution∫302x5+x4−2x3+2x2+1(x2+1)(x4−1)dx
View SolutionIf x=12 and if 1−2x1−x+x2+2x−4x31−x2+x4+4x3−8x71−x4+x6+...∞=k, then
View Solutionहल कीजिए ∫322x5+x4−2x3+2x2+1(x2+1)(x4−1)dx
View SolutionEvaluate ∫322x5+x4−2x3+2x2+1(x2+1)(x4−1)dx
View SolutionEvaluate: ∫322x5+x4−2x3+2x2+1(x2+1)(x4−1)dx
View SolutionSimplify: (x3−2x2+3x−4)(x−1)− (2x−3)(x2−x+1)
View SolutionEvaluate ∫322x5+x4−2x3+2x2+1(x2+1)(x4−1)dx
View Solution