A(6.1), B(8.2), C(9.4) & D(P, 3) ಬಿಂದುಗಳು ಸಮಾಂತರ ಚತುರ್ಭುಜದ ಅನುಕ್ರಮ ತೃಂಗಗಳಾದರೆ 'P'ಯ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
Step by step video & image solution for A(6.1), B(8.2), C(9.4) & D(P, 3) ಬಿಂದುಗಳು ಸಮಾಂತರ ಚತುರ್ಭುಜದ ಅನುಕ್ರಮ ತೃಂಗಗಳಾದರೆ 'P'ಯ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ಎರಡು ಧನಾತ್ಮಕ ಪೂರ್ಣಾಂಕಗಳು a ಮತ್ತು b ಗಳಾಗಿದ್ದು a=x3y2 ಮತ್ತು b=xy3 ಆದರೆ a ಮತ್ತು b ಯ ಮ.ಸಾ.ಅ.
View Solutionಈ ಕೆಳಗಿನ ಸಂಖ್ಯೆಗಳಲ್ಲಿ ಅಭಾಗಲಬ್ದ ಸಂಖ್ಯೆಯು.
View SolutionIf p=sin(A−B)sin(C−D),q=sin(B−C)sin(A−D), r=sin(C−A)sin(B−D) then (a) p+q−r=0 (b) p+q+r=0 p−q+r=0 (d) p3+q3+r3=3pqr
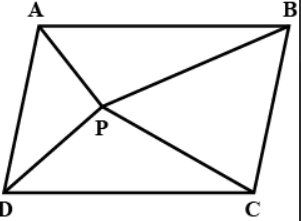
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View SolutionIf 2a+b+3c=1anda>0,b>0,c>0, then the greatest value of a4b2c2 is 19.48 b. 19.45 c. 194.48 d. 194.4□
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionIf AD is median of ABC and P is a point on AC such that ar (ADP): ar (ABD)=2:3, then ar(PDC):ar (ABC) is 1:5 (b) 1:5 (c) 1:6 (d) 3:5
View SolutionABCD is a cyclic quadrilateral whose diagonals AC and BD intersect at P. If AB=DC, prove that:
(i)PAB ≅PDC
(ii)PA=PD and PC=PB (iii) AD∣∣BC
View SolutionIf ab=bc=cd, thenb3+c3+d3a3+b3+c3 will be equal to ab b. bc c. cd d. da
View SolutionThe pH of an aqueous solution at 25∘C is 6.1 its p(OH) is :
View SolutionFor positive real numbers a,bc such that a+b+c=p, which one holds? (a) (p−a)(p−b)(p−c)≤827p3 (b)(p−a)(p−b)(p−c)≥8abc (c)bca+cab+abc≤p (d) none of these
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View SolutionABCD is a cyclic quadrilateral whose diagonals ACandBD intersect at P . If AB=DC, Prove that : PAB≅PDC PA=PDandPC=PB ADllBC
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
View Solution
