ABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that CQ=13BC. Prove that AQCP is a parallelogram.
To prove that quadrilateral AQCP is a parallelogram, we will follow these steps:
Step 1: Understand the Given Information
We have a parallelogram ABCD where:
- P is a point on AD such that AP=13AD
- Q is a point on BC such that CQ=13BC
Step 2: Use Properties of Parallelograms
Since ABCD is a parallelogram, we know:
- AD∥BC
- AD=BC
Step 3: Relate the Segments
From the information given:
- Since AP=13AD, it follows that PD=AD−AP=AD−13AD=23AD.
- Similarly, since CQ=13BC, we have BQ=BC−CQ=BC−13BC=23BC.
Step 4: Establish Parallelism
Since AD∥BC, we can conclude that:
- AP∥CQ because both segments are parts of lines that are parallel to each other.
Step 5: Establish Equality of Lengths
From the previous steps, we have:
- AP=13AD and CQ=13BC
- Since AD=BC (as sides of the parallelogram), we can say AP=CQ.
Step 6: Conclude that AQCP is a Parallelogram
Now we have:
- AP∥CQ (both are parallel)
- AP=CQ (both are equal)
By the definition of a parallelogram, if one pair of opposite sides are both equal and parallel, then the quadrilateral AQCP is a parallelogram.
Final Conclusion
Thus, we have proved that AQCP is a parallelogram.
---
We have a parallelogram ABCD where:
- P is a point on AD such that AP=13AD
- Q is a point on BC such that CQ=13BC
Since ABCD is a parallelogram, we know:
- AD∥BC
- AD=BC
From the information given:
- Since AP=13AD, it follows that PD=AD−AP=AD−13AD=23AD.
- Similarly, since CQ=13BC, we have BQ=BC−CQ=BC−13BC=23BC.
Since AD∥BC, we can conclude that:
- AP∥CQ because both segments are parts of lines that are parallel to each other.
From the previous steps, we have:
- AP=13AD and CQ=13BC
- Since AD=BC (as sides of the parallelogram), we can say AP=CQ.
Now we have:
- AP∥CQ (both are parallel)
- AP=CQ (both are equal)
Thus, we have proved that AQCP is a parallelogram.
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram. P is a point on AD such that AP=13AD and Q is a point on BC such that CQ=13BP . Prove that AQCP is a parallelogram.
View SolutionABCD is a parallelogram. E is a point on BA such that BE=2 EA and F is a point on DC such that DF=2 FC. Prove that AECF is a parallelogram whose area is one third of the area of parallelogram ABCD.
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
View SolutionABCD is a parallelogram. P is the mid-point of AB.BD and CP intersect at Q such that CQ:QP=3:1. If ar (PBQ)=10 cm2, find the area of parallelogram ABCD
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
View SolutionIn Figure, X, Y are the mid-points of opposite sides AB and DC of a parallelogram ABCD.AY and DX are joined intersecting in P;CX and BY are joined intersecting in Q . Show that
(i) AXCY is a parallelogram
(ii) DXBY is a parallelogram
(iii)PXQY is a parallelogram
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O , a time is drawn to intersect AD at P and BC at Q . Show that PQ divides the parallelogram into two parts of equal area.
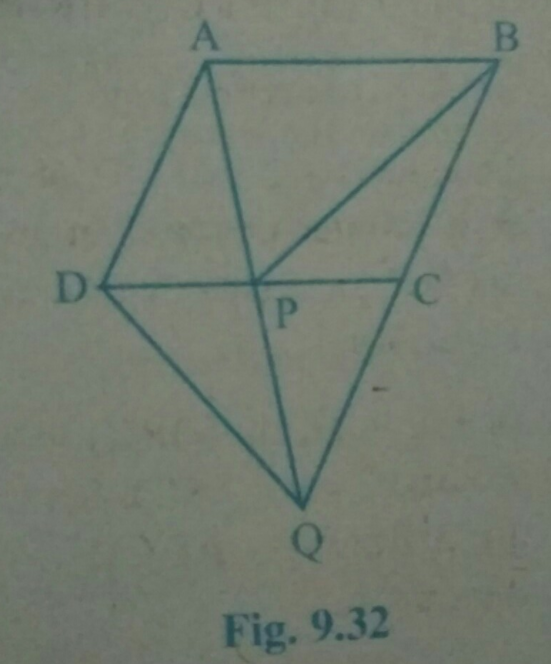
View SolutionIn Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such thatAD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
View SolutionABC is a triangle in which AB=AC and P is a point on AC . Through C a line is drawn to intersect BP produced at Q such that ∠ABQ= ∠ACQ. Prove that: ∠AQC=90∘+12∠BAC
View Solution
