Number of roots of $| sin | x | | = x + | x | in [- 2 π, 2 π]$ , is

A

2

B

3

C

4

D

6

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

The total number of solutions of the given equation is equal to the number of points of intersection of the curves.
$y = | sin | x | | and y = x + | x | = {\begin{matrix} 2 x & x \leq 0 0 & x < 0 \end{matrix}$

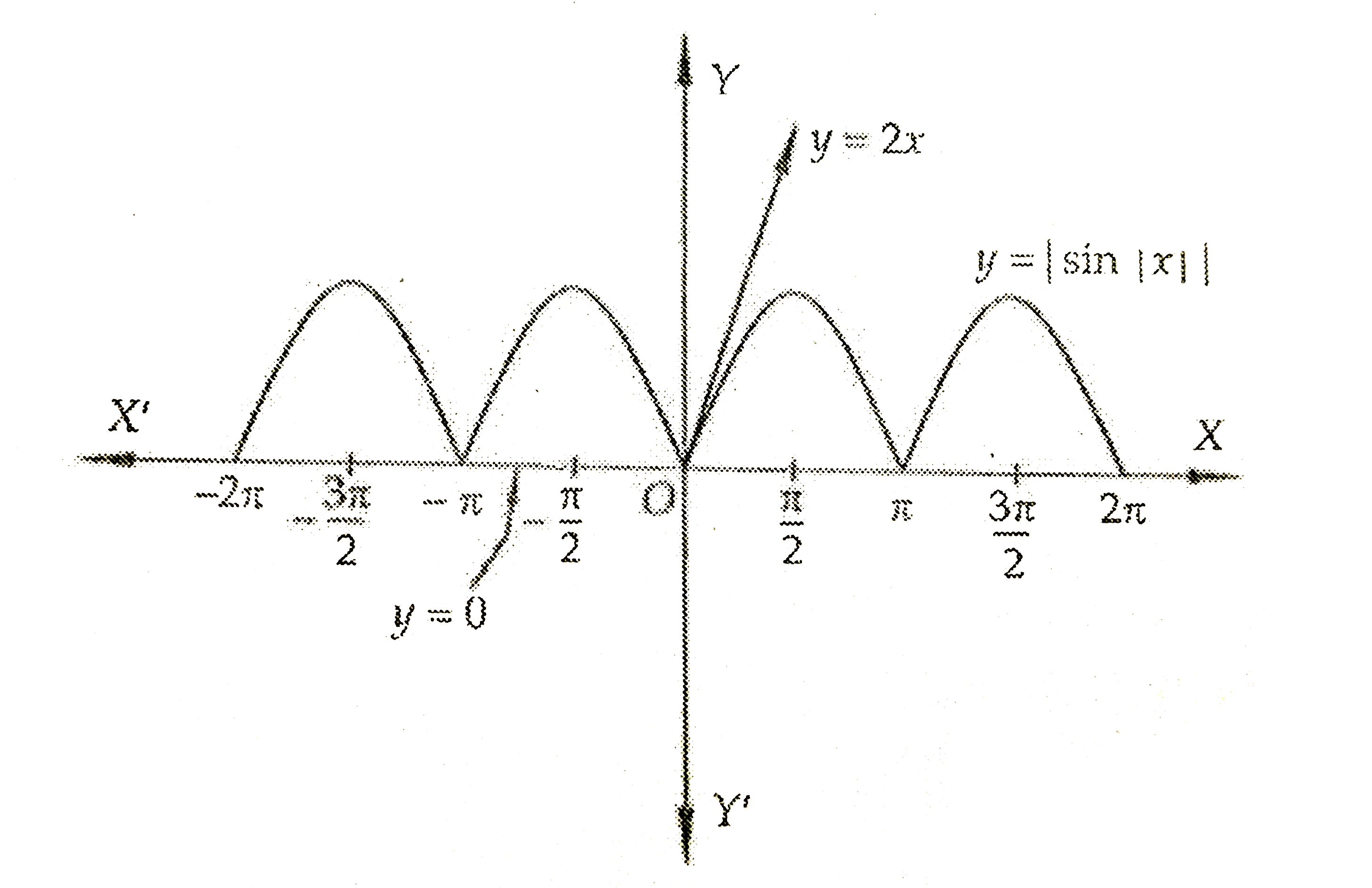
Clearly, these two curves intersect at x=0, $- π$ and $- 2 π$ . Hence, there are three solutions of the given equation.

|

Updated on:21/07/2023

Class 12 MATHS MISCELLANEOUS EQUATIONS AND INEQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Number of roots of $| sin | x | | = x + | x | \forall x \in [- 2 π, 2 π]$ is
A $0$
B $1$
C $2$
D $3$
Question 2 - Select One
The number of solution of the equation $| sin x | = | cos 3 x |$ in $[- 2 π, 2 π]$ is
A32
B28
C24
D30
Question 3 - Select One
If $f (x) = \frac{{cos}^{2} x + {sin}^{4} x}{{sin}^{2} x + {cos}^{4} x}$ for $x \in R$ then number of solution of the equation $| sin x | = f (x)$ in $[- 2 π, 2 π]$ is
A2
B3
C4
D5

OBJECTIVE RD SHARMA-MISCELLANEOUS EQUATIONS AND INEQUATIONS -Chapter Test

Home
Ask Doubt
Profile