The altitude of a cone is 20 cm and its semi-vertical angle is 30∘. If the semi-vertical angle is increasing at the rate of 2∘ per second, then the radius of the base is increasing at the rate of
30 cm/sec
1603cm/sec
10 cm/sec
160 cm/sec
The correct Answer is:B
Let θ be the semi-vertical angle and r be the radius of the cone at time t. Then,
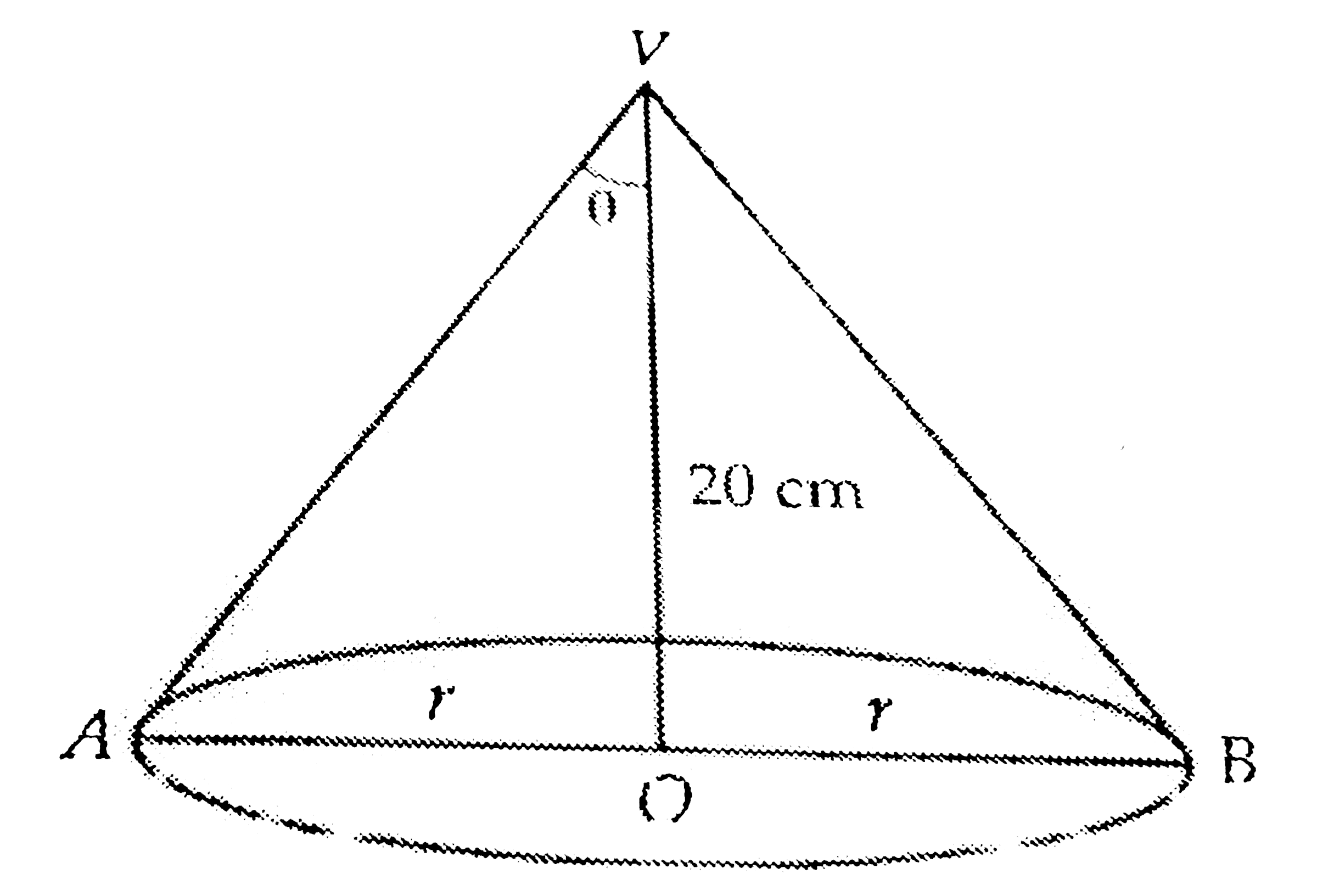
r=20tanθ
⇒drdt=20sec2θdθdt
⇒drdt=20sec230∘×2 [∵θ=30∘anddθdt=2(given)]
⇒drdt=20×43×2cm/sec=1603cm/sec
Topper's Solved these Questions
- DERIVATIVE AS A RATE MEASURER BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise
26 Videos
- DERIVATIVE AS A RATE MEASURER BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise
26 Videos
- DEFINITE INTEGRALSBOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 2
60 Videos
- DIFFERENTIAL EQUATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Chapter Test
30 Videos
Similar Questions
The altitude of a cone is 20 cm and its semi-vertical angle is 30∘. If the semi-vertical angle is increasing at the rate of 2∘ per second, then the radius of the base is increasing at the rate of
View SolutionThe radius of spherical balloon is increasing at the rate of 5 cm per second. At what rate is the surface of the balloon increasing, when the radius is 10 cm?
View Solution
Knowledge Check
Area of circular blot of ink is increasing at the rate of 2cm2/sec.When the area of the blot is 4cm2,its radius is increasing at the rate of
A12πcm/secB12√πcm/sec.C12π2cm/sec.Dπ√2cm/sec.If the radius of a circle is 2 cm and is increasing at the rate of 0.5 cm/sec., then the rate of increase of its area is
Aπcm2/secB2πcm2/secC3πcm2/secD4πcm2/secPerimeter of square increases at the rate of 0.4cm/sec. When the side is 20 cm, its area increases at the rate of
A0.4cm2/sec.B−25cm2/sec.C0.2cm2/sec.D4cm2/sec.
Perimeter of square increases at the rate of 0.4cm/sec. When the side is 20 cm, its area increases at the rate of
View SolutionIf the radius of circle is increasing at the rate of 0.5 cm/s, then the rate of increase of its circumference is______
View SolutionThe diameter of a circle is increasing at the rate of 1 cm/sec. When its radius is π, the rate of increase of its area, is
View SolutionIf the edge of a cube increases at the rate of 60 cm per second, at what rate the volume is increasing when the edge is 90 cm
View SolutionIf the edge of a cube increases at the rate of 60cm per second, at what rate the volume in increasing when the edge is 90cm
View Solution
