If a particle moves along a line by S=√1+t then its acceleration is proportional to
square of the velocity
cube of the displacement
cube of the velocity
square of the displacement
The correct Answer is:C
We have,
s=√1+t
⇒dsdt=12√1+t
⇒dsdt=12s
⇒d2sdt2=−12s2dsdt=−12s2×12s=−14s3
⇒d2sdt2=−2×(12s)3=−2(dsdt)3
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise26videos
DERIVATIVE AS A RATE MEASURER
- BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise26videos
DERIVATIVE AS A RATE MEASURER
- BOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 260videos
DEFINITE INTEGRALS
- BOOK - OBJECTIVE RD SHARMACHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Chapter Test30videos
DIFFERENTIAL EQUATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle moves in a straight line so that s=√t, then its acceleration is proportional to
A(velocity)3BvelocityC(velocity)2D(velocity)3/2 - Question 2 - Select One
A particle moves in a straight line so that s=√t, then its acceleration is proportional to :
A(velocity)3BvelocityC(velocity)2D(velocity)3/2 - Question 3 - Select One
A particle moves in a straight line so that s=√t, then its acceleration is proportional to :
A(velocity)3BvelocityC(velocity)2D(velocity)3/2
For a particle moving along circular path, the radial acceleration ax is proportional to time t. If at is the tangential acceleration, then which of the following will be independent of time t.
View SolutionA particle moves along a straight line in such a way that its acceleration is increasing at the rate of 2m/s3. Its initial acceleration and velocity were zero. Then, the distance which it will cover in the 3rd second (t=2 to t=3 sec) is :
View SolutionThe velocity –position graph of a particle moving along a straight line is shown. Then acceleration of the particle at s = 15 m is :
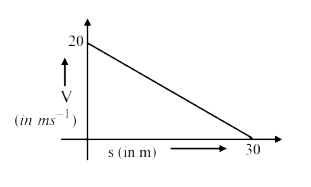 View Solution
View SolutionA particle is moving along X-axis Its acceleration at time t is proportional to its velocity at that time. The differential equation of the motion of the particle is
View SolutionAcceleration time graph of a particle moving along a straight line is given. Then average acceleration between t=0 & t=4 is :−
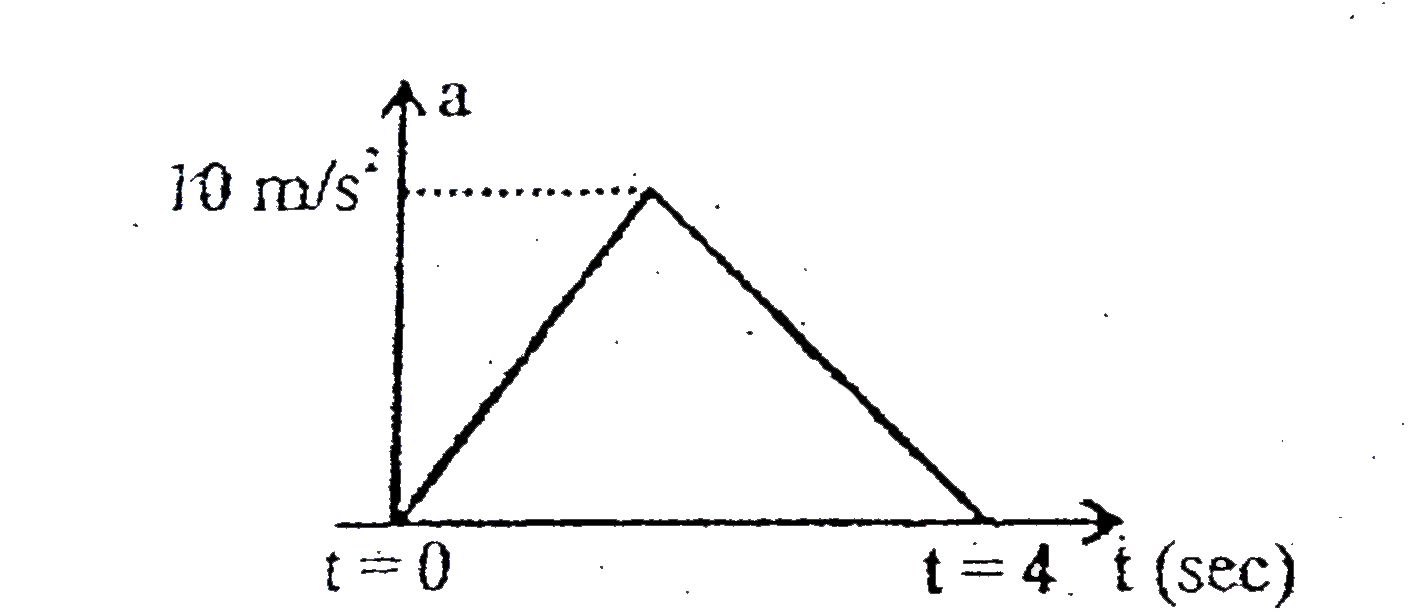 View Solution
View Solution

