If (1×2×3×4×....×n!) = n, then (14! - 13! - 12!) is equal to
14×12×(12!)
14×12×(13!)
14×13×(13!)
13×12×(12!)
The correct Answer is:A
Step by step video, text & image solution for If (1xx 2 xx 3 xx 4xx .... xx n!) = n, then (14! - 13! - 12!) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - HIGHER SKILL LEVEL QUESTIONS19videos
PERMUTATIONS AND COMBINATIONS
- BOOK - ARIHANT SSCCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - HIGHER SKILL LEVEL QUESTIONS19videos
PERMUTATIONS AND COMBINATIONS
- BOOK - ARIHANT SSCCHAPTER - PERMUTATIONS & COMBINATIONS EXERCISE - FINAL ROUND38videos
PERMUTATIONS & COMBINATIONS
- BOOK - ARIHANT SSCCHAPTER - PIE CHART EXERCISE - Exercise Higher Skill Level Questions15videos
PIE CHART
Similar Questions
Knowledge Check
- Question 1 - Select One
If 1×2×3×…….×n is denoted by
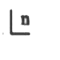 , then
, then 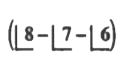 is equal to : A
is equal to : A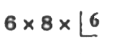 B
B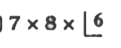 C
C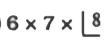 D
D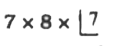
- Question 2 - Select One
If 17×13=4and16×14=2, then 29×23= ?
A5B7C6D8 - Question 3 - Select One
The statement P(n): ''1×1!+2×2!+3×3!+...+n×Xn!=(n+1)!−1''is
Atrue for all n>1Bnot true for any nCtrue for all n ∈ NDNone of these
If 11×2+12×3+13×4+………..+1n(n+1)=99100 then what is the value of n?
View SolutionLet P(n):2n<(1×2×3×.....×n),n∈N. Then the smallest natural number n, for which P(n) is true is
View SolutionThe sum of the last 10 digits of the sum of the expression:
(11×22×33×44×55)+(16×27×38×49×510)+(111×212×313×414×515)+……
+(196×297×398×499×5100) is :View SolutionIf A {1,2},B={1,3}, then (A×B)∪(B×A) is equal to
View SolutionIf the product of 1×2×3×4×…n contains 68 zeros in the end of the number. Then the maximum possible number of values of n is:
View Solution

