The relation p(p+1)>1 is valid when :
p≥−1
p>−1
p<−1
−1<p<0
The correct Answer is:C
To solve the inequality pp+1>1, we will follow these steps:
Step 1: Rewrite the inequality
Start by rewriting the inequality:
pp+1>1
Step 2: Move all terms to one side
Subtract 1 from both sides:
pp+1−1>0
Step 3: Combine the fractions
To combine the fractions, we need a common denominator:
p−(p+1)p+1>0
This simplifies to:
p−p−1p+1>0
Which further simplifies to:
−1p+1>0
Step 4: Analyze the inequality
The fraction −1p+1 is greater than 0 when the denominator p+1 is negative (since the numerator is negative). Therefore, we need:
p+1<0
Step 5: Solve for p
Solving the inequality:
p<−1
Conclusion
The relation pp+1>1 is valid when p<−1.
Start by rewriting the inequality:
pp+1>1
Subtract 1 from both sides:
pp+1−1>0
To combine the fractions, we need a common denominator:
p−(p+1)p+1>0
This simplifies to:
p−p−1p+1>0
Which further simplifies to:
−1p+1>0
The fraction −1p+1 is greater than 0 when the denominator p+1 is negative (since the numerator is negative). Therefore, we need:
p+1<0
Solving the inequality:
p<−1
The relation pp+1>1 is valid when p<−1.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - LEVEL 2123videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - FINAL ROUND116videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - EXERCISE - MISCELLANEOUS140videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - FUNCTIONS AND GRAPHEXERCISE - Final Round40videos
FUNCTIONS AND GRAPH
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)52videos
GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
The relation pP+1>1 is valid when :
Ap≥−1Bp>−1Cp<−1D−1<p<0 - Question 2 - Select One
The variation of p(x/m) as a function of p when Lanmuir's is isotherm is valid is :
A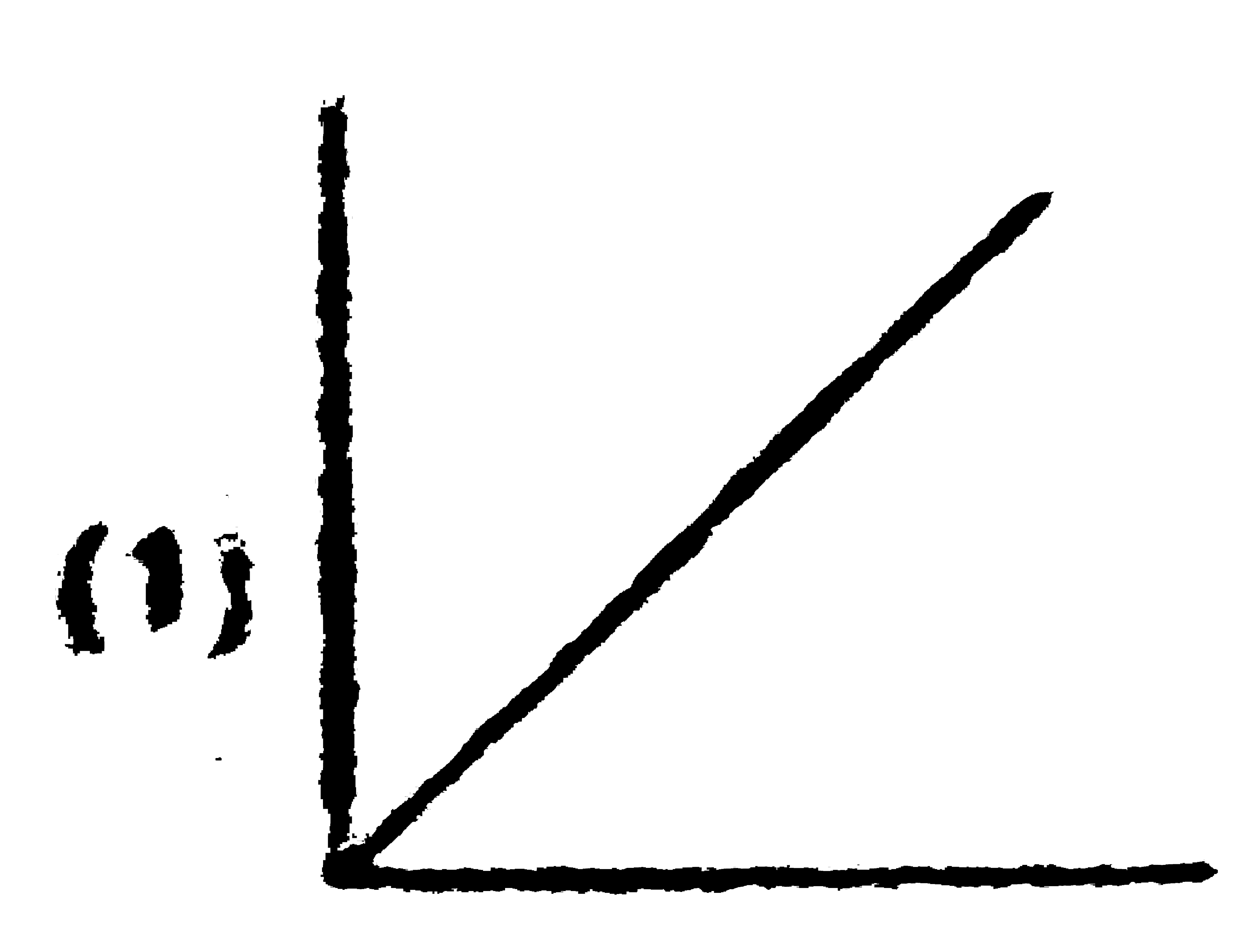 B
B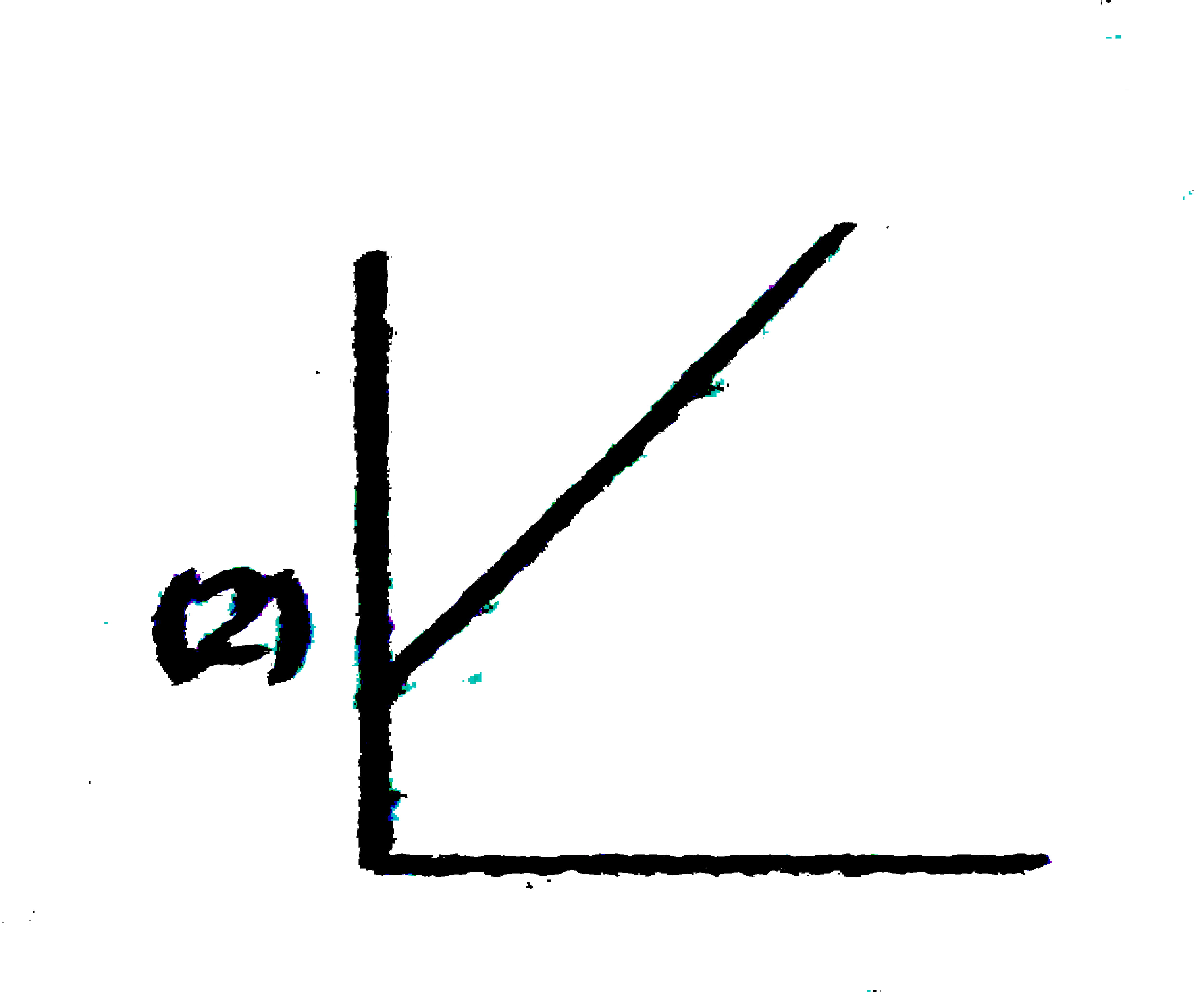 C
C D
D
- Question 3 - Select One
The appropriate value of P for the relation (P!+1)=(P+1)2 is :
A3B4C5Dnone of these
Under which of the following condition is the relation ΔH=ΔU+PΔV valid for a closed system at
View SolutionLet P(x) be quadratic polynomical with real coefficient such tht for all real x the relation 2(1+P(x))=P(x−1)+P(x+1) holds. If P(0)=8 and P(2)=32 then
Sum of all coefficients of P(x) can not beView SolutionFor every p, q positive integers at x = 0 or x = 1, the valid relation can be :
View SolutionUnder which of the following conditions is the relation, ΔH=ΔE+PΔV valid for a system :-
View SolutionUnder which of the following conditions is the relation, ΔH=ΔE+PΔV valid for a system :-
View Solution

