ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
A)AN=√3AB
B)AN=2AB
C)AN2=32AB2
D)AN2=2AB2
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the Parallelogram
We have a parallelogram ABCD, where opposite sides are parallel and equal in length. This means:
- AB is parallel to CD
- AD is parallel to BC
Step 2: Identify the Midpoint
M is the midpoint of side BC. Therefore, we can say that:
- BM = MC
Step 3: Extend the Lines
We extend lines AB and DM to meet at point N.
Step 4: Apply Thales' Theorem
Since M is the midpoint of BC, we can apply Thales' theorem. According to this theorem, if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
In our case:
- Since AD is parallel to BC and M is the midpoint of BC, we can say that:
ANAB=AMBM
Step 5: Establish Ratios
Since M is the midpoint of BC, we have:
- BM = MC, which means AM is equal to BM (because M divides BC into two equal parts).
Thus, we can say:
AMBM=1
Step 6: Relate AN and AB
From the ratios established, we can write:
ANAB=2(because AN = AB + BN and BN = AB)
This implies:
AN=2×AB
Conclusion
Thus, the relation between AN and AB is:
AN=2×AB
Final Answer
The correct option is B: AN=2×AB.
---
We have a parallelogram ABCD, where opposite sides are parallel and equal in length. This means:
- AB is parallel to CD
- AD is parallel to BC
M is the midpoint of side BC. Therefore, we can say that:
- BM = MC
We extend lines AB and DM to meet at point N.
Since M is the midpoint of BC, we can apply Thales' theorem. According to this theorem, if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally.
- Since AD is parallel to BC and M is the midpoint of BC, we can say that:
ANAB=AMBM
Since M is the midpoint of BC, we have:
- BM = MC, which means AM is equal to BM (because M divides BC into two equal parts).
AMBM=1
From the ratios established, we can write:
ANAB=2(because AN = AB + BN and BN = AB)
This implies:
AN=2×AB
Thus, the relation between AN and AB is:
AN=2×AB
The correct option is B: AN=2×AB.
Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.4
10 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.5
60 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.2
100 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
Knowledge Check
In the given figure, ABCD is a parallelogram and M, N are the mid-points of AB and CD. The value of θ is
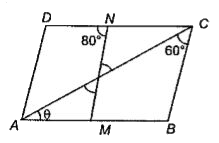 A20*B30*C40*D10*
A20*B30*C40*D10*In the given figure, ABCD is a parallelogram and M, N are the mid-points of AB and CD. The value of θ is
 A20∘B30∘C40∘D10∘
A20∘B30∘C40∘D10∘ABCD is a parallelogram and L is a point on DB . The produced line AL meets BC at M and DC produced at N .
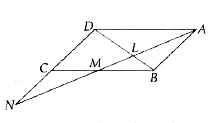
Given that DL =3LB , find ABCN .A3/2B1/2C4/5D1/4
In the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
View SolutionABCD is a parallelogram. L and M are respectively mid points of sides AB and DC. Prove that LD and MB trisects diagonals AC.
View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH.
View SolutionABCD is a parallelogram, P is the mid point of AB. BD and CP intersects at Q such that CQ:QP=3:1. If ar(ΔPBQ)=10cm2, find the area of parallelogram ABCD.
View SolutionABCD is a parallelogram, E and F are the mid-points of BC and CD. Find the ratio of area of parallelogram ABCD and ΔAEF
View Solution