In the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
In∠ABEand∠CDL
AB=CD
∠AEB=∠CLD
∠BAE=∠DCL
∠ABE≅∠CDL(ASA)
AE=CL
BE=DL
In∠AEBand∠ADF
∠A=∠A
∠AEF=∠ADF
∠ABE=∠AFD
∠AEB≅∠ADF(AAA)
ADAE=DFBE=AFAB=2
DF=2BE,AF=2AB
DF=2DL,AF=2CD.
Similar Questions
In parallelogram ABCD, E is mid-point of CD and through D, a line is drawn parallel to EB to meet CB produced at point G and to cut AB at point F. Prove that :
DG = 2EB
View SolutionIn parallelogram ABCD, E is mid-point of CD and through D, a line is drawr parallel to EB to meet CB produced at point G and to cut AB at point F. Prove that:
2×AD=GC
View SolutionIn the given figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.

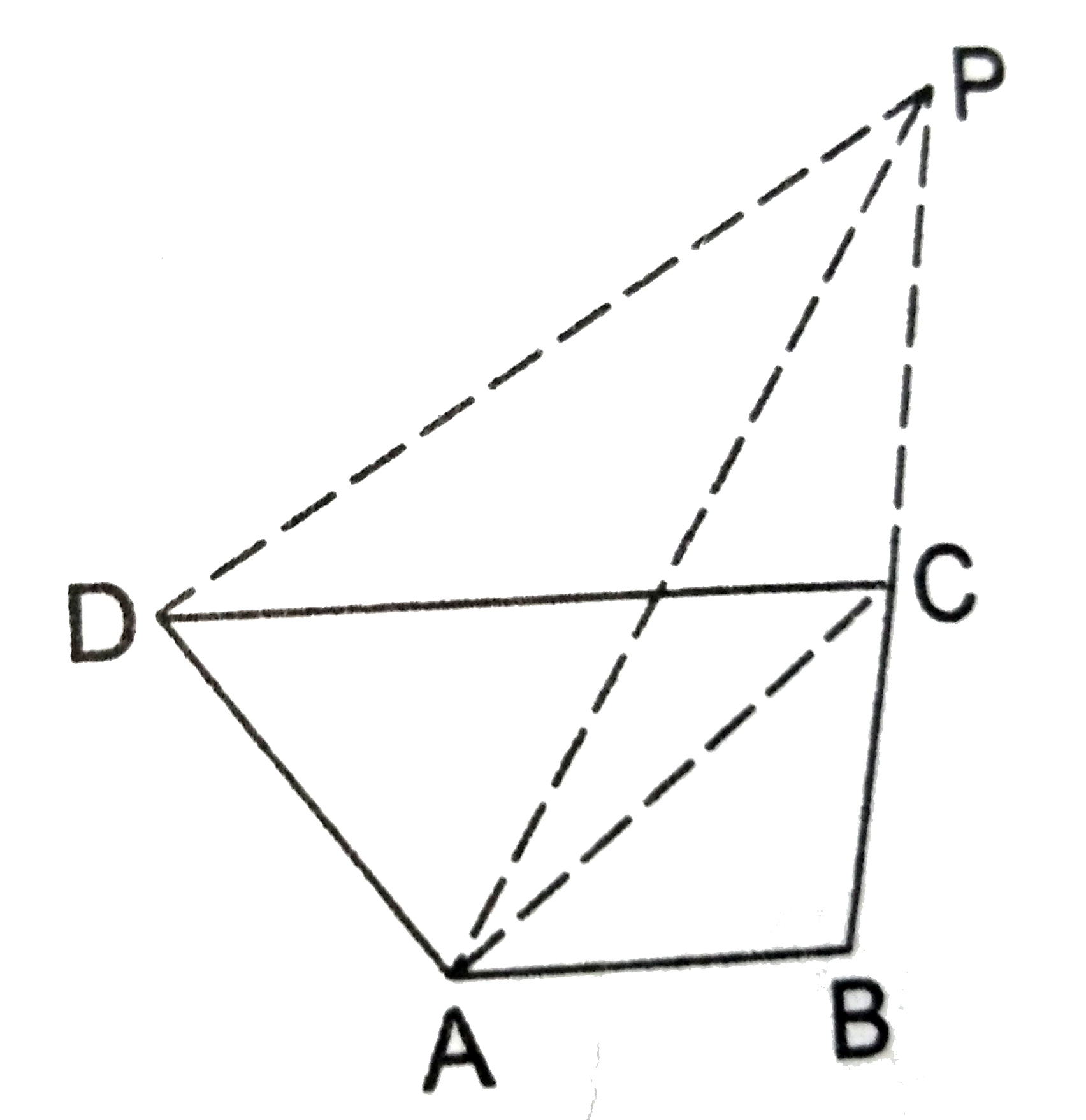
View SolutionIn the adjoining figure, ABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P .
Prove that ar(△ABP)=ar(qaud. ABCD).
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that :
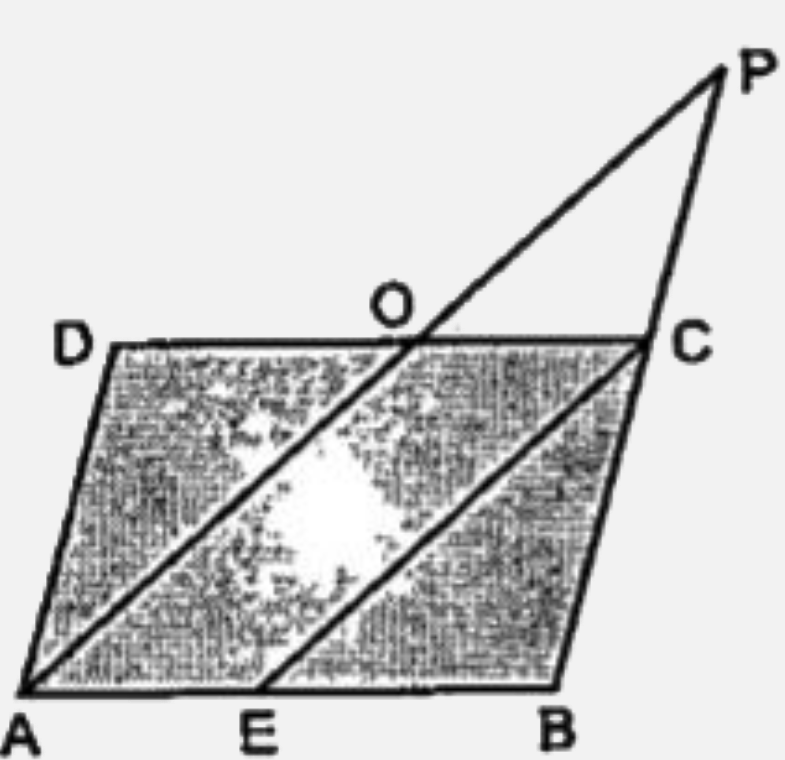
BP=2AD
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:
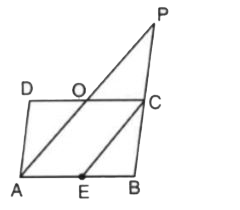
PB=2AD
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View SolutionIn a trapezium ABCD, AB/DC, E is mid-point of aD. A line through E and parallel to AB intersects BC at point F. Show that:
2EF=AB+DC
View SolutionAB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
View SolutionAB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
View Solution
