In the given figure the two chords AC and BC are equal. The radius OC intersect AB at M, then AM:BM is :
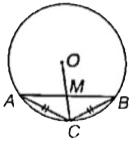
1:1
√2:3
3:√2
none of these
The correct Answer is:A
Step by step video, text & image solution for In the given figure the two chords AC and BC are equal. The radius OC intersect AB at M, then AM : BM is : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 1)54videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)52videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.410videos
GEOMETRY
- BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 240videos
FUNDAMENTALS
- BOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions18videos
HCF AND LCM
Similar Questions
Knowledge Check
- Question 1 - Select One
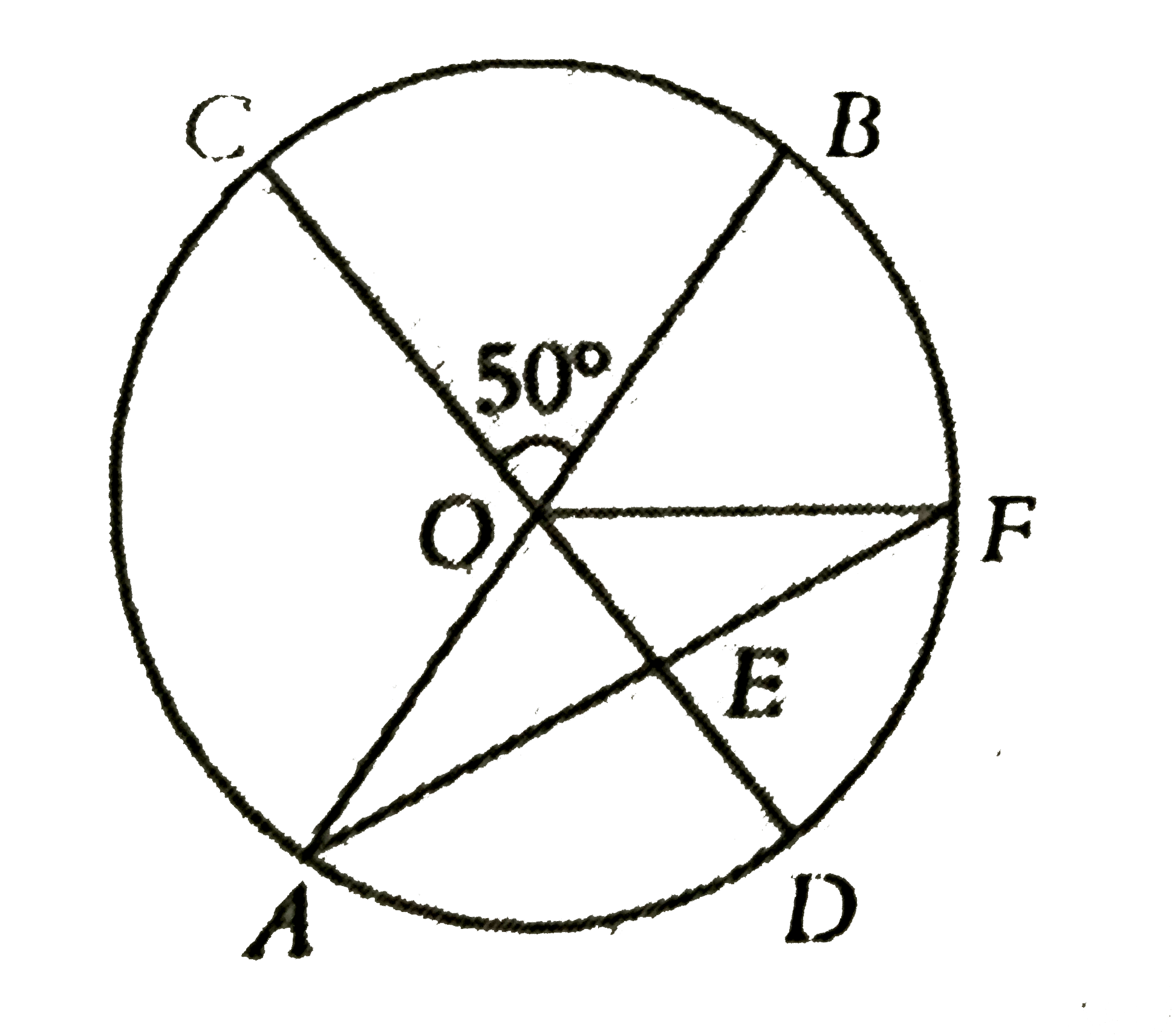
In the above figure , O is the centre of the circle, AB and CD are diameters. ∠COB=50∘=50∘ . If E is the midpoint of AF, then find ∠ADFA65∘B55∘C70∘D50∘
In the given figure, chords AB and CD are intersecting each other at point L. Find the length of AB.
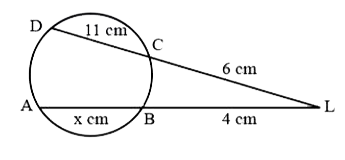 View Solution
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.
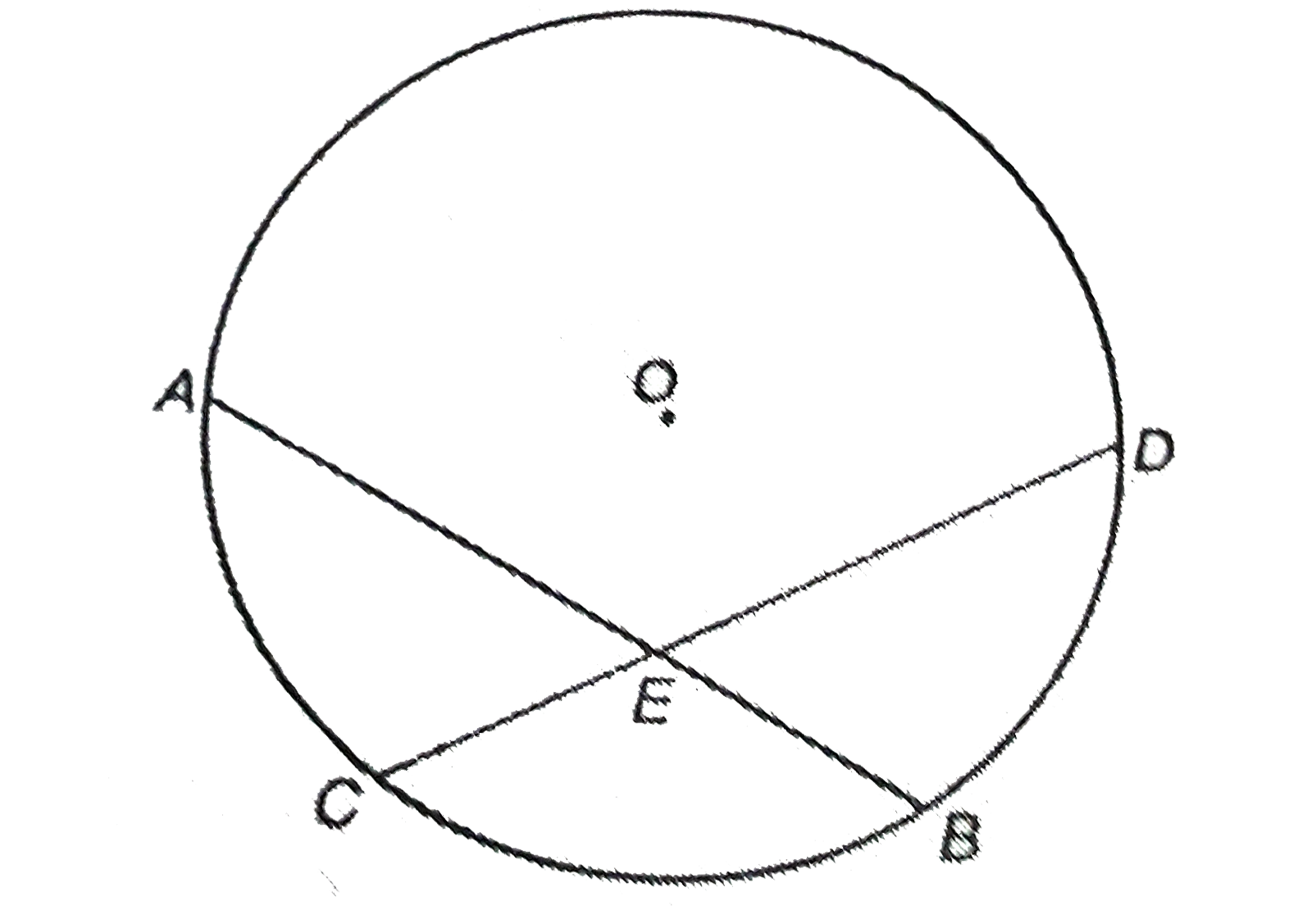 View Solution
View SolutionIn the concerned diagrams, chords AB and CD are parallel and radius OR bisects the chord AB at P and CD at Q. Radius OC when extended to a point T in order to meet the tangent TR it intersects the chord AB at S. If OP:OS=8:17, find OC:OT
 View Solution
View SolutionIn the given figure, AC is the diameter, AB and AD are equal chords. If ∠AED=110∘, then find ∠BAD.
 View Solution
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect point O. Prove that :
AB+BC+CD+DA<2(AC+BD)
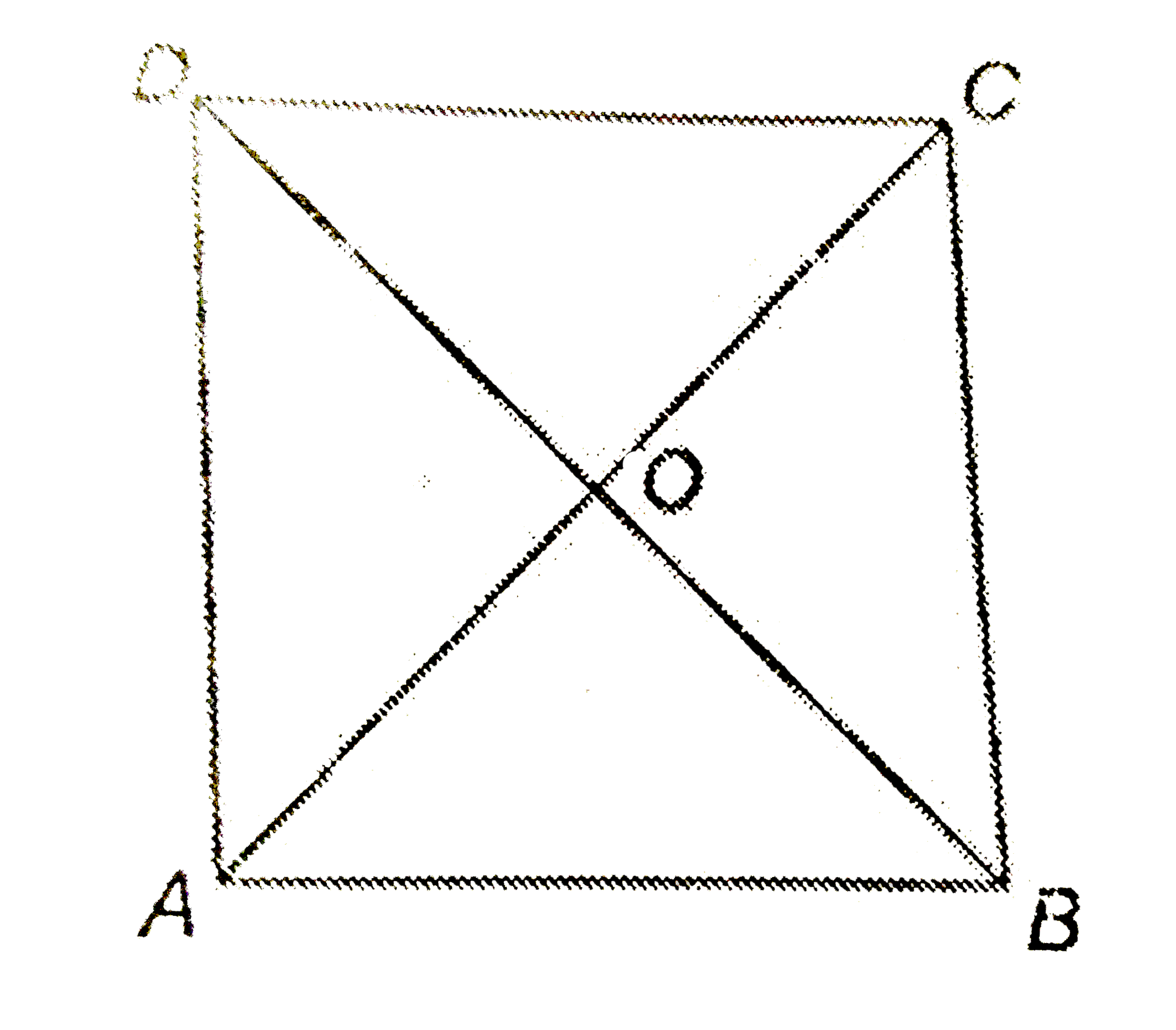 View Solution
View SolutionIn the given figre, AB = AC and OB = OC. Then, ∠ABO:∠ACO=?
 View Solution
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View Solution


