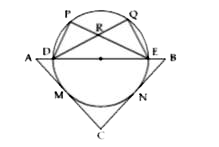
ABC is an isosceles triangle and AC, BC are the tangent at M and N respectively. DE is the diameter of the circle. ∠ADP=∠BEQ=100∘. What is the value of ∠PRD?
60∘
50∘
20∘
20∘
The correct Answer is:C
Step by step video & image solution for ABC is an isosceles triangle and AC, BC are the tangent at M and N respectively. DE is the diameter of the circle. angleADP=angleBEQ=100^(@). What is the value of anglePRD? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A circle is inscribed in a triangle ABC. It touches the sides AB and AC at M and N respectively. If O is the centre of the circle and ∠A=70∘ , then what is ∠MON equal to ?
View SolutionABC is an isosceles triangle in which AB = AC. Prove that the tangent to the circum-circle at A is parallel to BC.
View Solution
Knowledge Check
ABC is an isosceles triangle such that AB = AC and ∠B=35∘. AD is the medium to the base BC. Then ∠BAD is:
A55∘B70∘C35∘D110∘ABC is an isosceles triangle inscribed in a circle. If AB=AC12√5 and BC = 24 cm then radius of circle is:
A10 cm.B15 cm.C12 cm.D14 cm.The equations of two equal sides AB and AC of an isosceles triangle ABC are x + y = 5 and 7x - y = 3 respectively. What will be the equation of the side BC if area of triangle ABC is 5 square units.
Ax + 3y - 1 = 0Bx - 3y + 1 = 0C2x - y = 5Dx + 2y = 5
ABC is an isosceles triangle inscribed in a circle. If AB=AC12√5 and BC = 24 cm then radius of circle is:
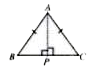
View SolutionABC is an isosceles triangle with AB= AC. Draw AP⊥BC to show that ∠B=∠C.
View SolutionABC is an isosceles triangle with AC = BC. If AB2=2AC2, prove that ABC is a right triangle.
View SolutionABC is an isosceles triangle with AC = BC. If AB2−2AC2=0, prove that ABC is right triangle.
View SolutionABC is an isosceles triangle with AB = AC. Draw AP⊥BC to show that ∠B=∠C.
View Solution
