A huge piston in a machine is undergoing, vertical S.H.M approximately with a frequency of 1 s−1. A 5 kg block is placed on the piston. iF the block and the piston move together, determine the maximum amplitude of the piston S.H.M. such that block remains in contact with piston
take, g = 9.8 m/s2
To solve the problem, we need to determine the maximum amplitude of the piston undergoing simple harmonic motion (SHM) such that a 5 kg block remains in contact with it.
1. Identify the Forces Acting on the Block:
- The block experiences a downward gravitational force, Fg=mg, where m=5kg and g=9.8m/s2.
- The maximum force due to SHM acting on the block is the upward force due to the acceleration of the piston.
2. Calculate the Gravitational Force:
Fg=mg=5kg×9.8m/s2=49N
3. Understand the Condition for the Block to Remain in Contact:
- For the block to remain in contact with the piston, the upward acceleration of the piston must not exceed the acceleration due to gravity. Thus, the maximum upward acceleration a must satisfy:
a≤g
4. Relate Acceleration to Amplitude and Frequency:
- The maximum acceleration a in SHM is given by:
a=ω2A
where ω is the angular frequency and A is the amplitude.
- The angular frequency ω can be calculated from the frequency f:
ω=2πf
Given that f=1s−1:
ω=2π×1=2πrad/s
5. Set Up the Inequality:
- Now we can set up the inequality:
ω2A≤g
Substituting ω and g:
(2π)2A≤9.8
6. Calculate the Maximum Amplitude:
- First, calculate (2π)2:
(2π)2=4π2≈39.478
- Now, substituting this value into the inequality:
39.478A≤9.8
- Solving for A:
A≤9.839.478≈0.248m
Final Answer:
The maximum amplitude of the piston SHM such that the block remains in contact with the piston is approximately 0.248m.
---
- The block experiences a downward gravitational force, Fg=mg, where m=5kg and g=9.8m/s2.
- The maximum force due to SHM acting on the block is the upward force due to the acceleration of the piston.
Fg=mg=5kg×9.8m/s2=49N
- For the block to remain in contact with the piston, the upward acceleration of the piston must not exceed the acceleration due to gravity. Thus, the maximum upward acceleration a must satisfy:
a≤g
- The maximum acceleration a in SHM is given by:
a=ω2A
where ω is the angular frequency and A is the amplitude.
- The angular frequency ω can be calculated from the frequency f:
ω=2πf
Given that f=1s−1:
ω=2π×1=2πrad/s
- Now we can set up the inequality:
ω2A≤g
Substituting ω and g:
(2π)2A≤9.8
- First, calculate (2π)2:
(2π)2=4π2≈39.478
- Now, substituting this value into the inequality:
39.478A≤9.8
- Solving for A:
A≤9.839.478≈0.248m
The maximum amplitude of the piston SHM such that the block remains in contact with the piston is approximately 0.248m.
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - PRACTICE PROBLEMS
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - PRACTICE PROBLEMS 2
20 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
The vertical motion of a huge piston in a machine is approximately simple harmonic with a frequency of 0.50s−1. A block of 10 kg is placed on the pistion. What is the maximum amplitude of the pistion's SHM for the block and the piston to remain together ?
View SolutionThe vertical motion of a huge piston in a machine is approximately simple harmonic with a frequency of 0.50s−1. A block of 10 kg is placed on the pistion. What is the maximum amplitude of the pistion's SHM for the block and the piston to remain together ?
View Solution
Knowledge Check
What should be the maximum value of M so that the 4 kg block does not slip over the 5 kg block : (Take g=10m/s2)
 A12 kgB8 kgC10 kgD6 kg
A12 kgB8 kgC10 kgD6 kgA horizontal platform is undergoing vertical S.H>M of time period T. A block of mass M is placed on the platform . The maximum mplitude of the platform so that the block is not detached form it is
AgT22π⋅2BgT24π2C2gT22π2D4gT2π2An block rides on position that is moving vertically with simple harmonic motion. The maximum speed of the piston is 2m/s. At what minimum amplitude of motion will the block and piston separate? (g=10m/s2)
A20 cmB30cmC40 cmD50 cm
The vertical motion of a huge piston in a machine is approximately SHM with a frequency of 1Hz.A block of mass 20 kg is placed on the piston . What is the maximum amplitude of the piston's SHM for the block and the piston to remain together .
Hint : v=12π√km
Find k
For maximum displacement xmax=A
For maximum restoring force , F=−kA=−mg
∴A=mgk=mgmω2=gω2
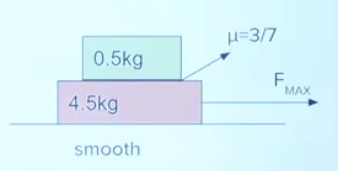
View SolutionFmax such that block moves together (g = 9.8 ms2)
View SolutionA block is resting on a piston which is moving vertically with simple harmonic motion of period 1.0 second. At what amplitude of motion will the block and piston separate? What is the maximum velocity of the piston at this amplitude?
View SolutionA block is resting on a piston which is moving vertically with simple harmonic motion of period 1.0 second. At what amplitude of motion will the block and pisto separate? What is the maximum velocity of the piston at this amplitude?
View SolutionA block of mass m is resting on a piston as shown in figure which is moving vertically with a SHM of period 1s. The minimum amplitude of motion at which the block and piston separate is :

View Solution
