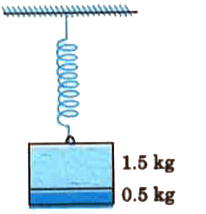
Two masses m1=1.0kgandm2=0.5kg are suspended together by a massless spring of force constant, k=12.5Nm−1. When they are in equillibrium position, m1 is gently removed. Calculate the angular frequency and the amplitude of oscillation of m2. Given g=10ms−2.
the given arrangement is shown in the below figure.
case I : When both blocks are suspended together
Let y1 be the extension produced in the case.
then, F=(1.5+0.5)g=ky1
⇒y12gk=2×1012=1.66 m
Case II : when only one block of mass 1.5 kg is supended
Let y2 be the extension produced in this case, Then,
1.5 g = ky2
y2=1.5k=1.5×1012
= 1.25 m
∴y1=y2=1.66−1.25=0.41m
This will be amplitude of oscillation of block of mass 1.5 kg
A = 0.41 m
Angular frequency ω=√k1.5=√121.5=2.83 rad/s
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - PRACTICE PROBLEMS
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - PRACTICE PROBLEMS 2
20 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
Two mass m1 and m2 are suspended from a massless spring of force constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. Find the angular frequency and amplitude of oscillations.
View SolutionTwo masses m1 and m2 are suspended together by a massless spring of constant K. When the masses are in equilibrium, m1 is removed without disturbing the system. Then the angular frequency of oscillation of m2 is -
View Solution
Knowledge Check
Two masses m1=1kgandm2=0.5kg are suspended together by a massless spring of spring constant 12.5Nm−1. When masses are in equilibrium m1 is removed without disturbing the system. New amplitude of oscillation will be
A30cmB50cmC80cmD60cmTwo masses 8 kg 4 kg are suspended together by a massless spring of spring constant 1000Nm−1 . When the masses are in equilibrium 8 kg is removed without disturbing the system. The amplitude of oscillation is
A0.5 mB0.08 mC0.4 mD0.04 mTwo masses m1and m2 are suspended from a spring of spring constant 'k'. When the masses are in equilibrium, m1 is gently removed. The angular frequency and amplitude of oscillation of m2 will be respectively
A√Km2,m1gKB√Km1,m2gKC√Km2,m2gKD√Km1,m1gK
Two masses m1 and m2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. The amplitude of oscillations is

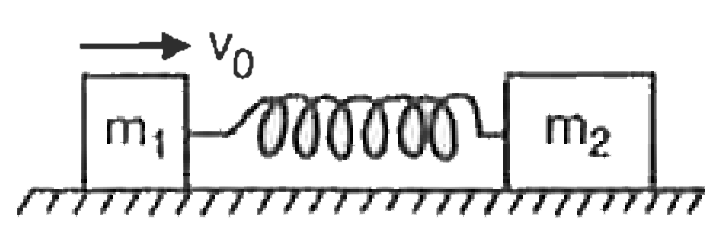
View SolutionTwo bodies with masses m1 = 1kg and m2= 2kg are connected by a spring of force constant k=24Nm−1. The left ball is imparted an initial velocity v0=12 cm/s. Find (a) the frequency of the oscillations (b) the energy and the amplitude of the osciallations.
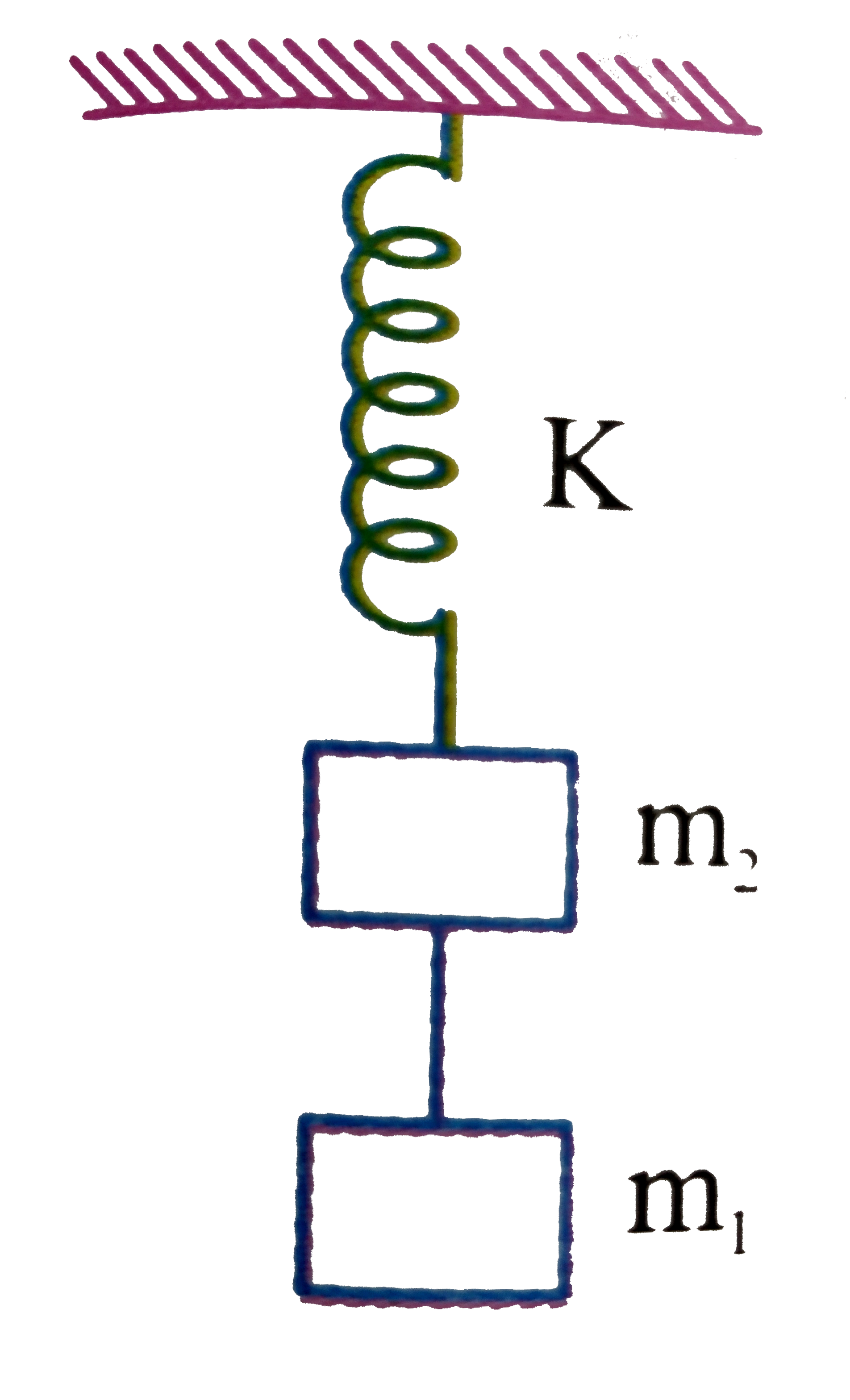
View SolutionTwo masses m1 and m2 are suspeded togther by a massless spring of spring constnat k (Fig). When the masses are in equilibrium, m1 is removed. Frequency and amplitude of oscillation of m2 are
View SolutionTwo masses M and m are suspended together by massless spring of force constant -k. When the masses are in equilibrium, M is removed without disturbing the system. The amplitude of oscillations.
View SolutionTwo masses m 1 and m 2 are suspended together by a massless spring of constant K . When the masses are in equilibrium, m 1 is removed without disturbing the system. The amplitude of oscillations is

View Solution
