Two identical springs (springs constant K) are connected together in three different ways. In which case will the spring factor of the oscillation of the body be least ?
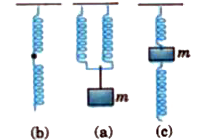
(a) If k1 is the spring factor of the combined system and R be the restoring force in each spring, then
2F=k1y
[where y is the displacement in each spring]
⇒F=−k12y …(i)
Also, for each spring
F = -Ky ...(ii)
comparing (i) and (ii), we get
K12=KorK1=2k
(b) In this case, the length of the spring is doubled, So, extension produced by the mass m will also be doubled, i.e, 2y. If k2 is the spring constant of the combined system, then
F=K2(2y)=−2k2y ...(iii)
Comparing (ii) and (iii)
2k2=KorK2=k/2
(c ) In this case, mass m produces an extension in the upper spring and a compression in the lower spring. So, each of the spring will give rise to the restoring force F in the same direction.
If K3 is the spring factor of the combined system in this case, then
2F=k3y
⇒F=k32y
Comparing (ii) and (iv),
K32=KorK3=2K
So, in case (b) spring constant will be least.
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - PRACTICE PROBLEMS
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - PRACTICE PROBLEMS 2
20 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
Two identical springs, each of spring factor k, may be connected in the following ways. Deduce the spring factor of the oscillation of the body in each case.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
Knowledge Check
A block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2kTwo identical springs of spring constant k each are connected in series and parallel as shown in figure. A mass M is suspended from them. The ratio of their frequencies of vertical oscillation will be
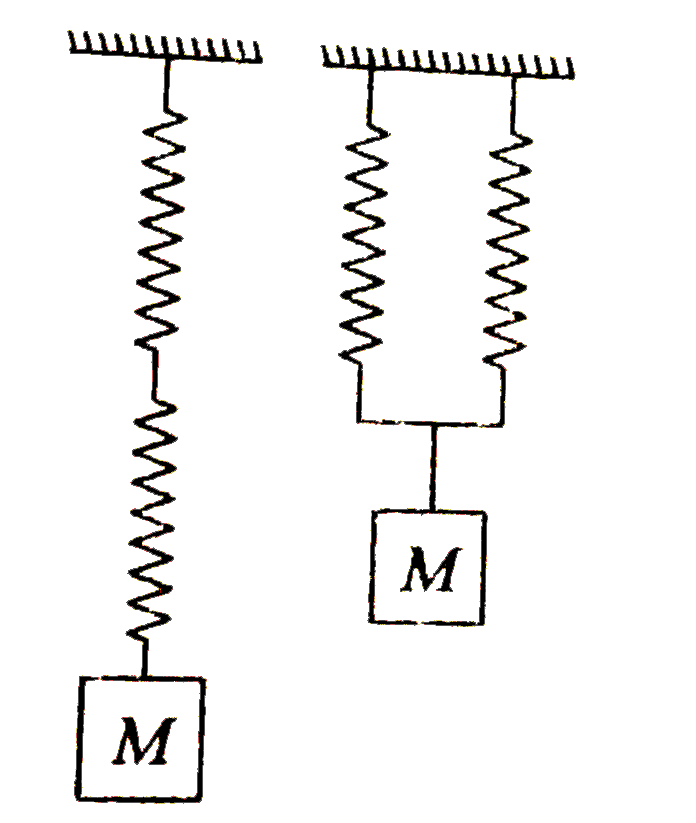 A1:2B2:1C4:1D1:4
A1:2B2:1C4:1D1:4A spring of spring constant k is cut in three equal pieces. The spring constant of each part will be
Ak3B3kCkDk6
Two identical spring of constant K are connected in series and parallel as shown in figure. A mass mis suspended from them. The ratio of their frequencies of vertical oscillations will be
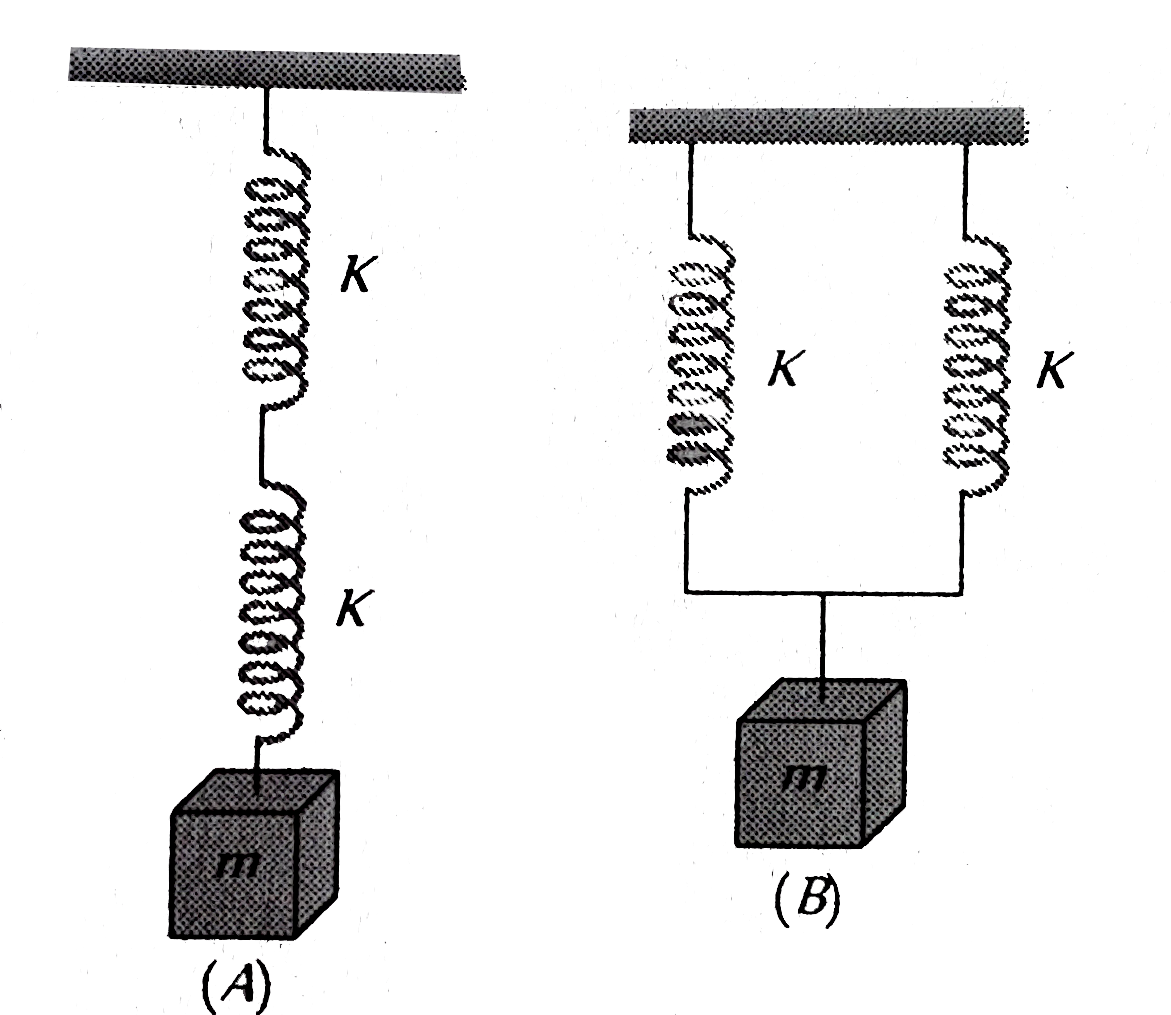
View SolutionTwo spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

View SolutionTwo identical massless springs A and B consist spring constant kA and kB respectively. Then :
View SolutionA light spring of spring constant k is cut into two equal halves. Each half is connected in parallel then net spring constant of the combination is :
View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View Solution