A spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

K = 1200 Nm−1
m = 3kg
Displacement = y = 2 cm = 0.02 m
(a) frequency =v=1T=12π√Km
=12×3.14√1200s=3.18s−1
(b) Maximum acceleration A=ω2y
ω=√Km
∴A=kym
=1200×0.023=8ms−2
( c ) maximum speed =v=yω
=0.02√Km=0.02√12003=0.4ms−1
Topper's Solved these Questions
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:NCERT (Additional Exercises)
Explore 6 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:NCERT Exemplar Problems Subjective Question (Multiple Choice Questions (Type-I))
Explore 11 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:TOUGH & TRICKY PROBLEMS
Explore 9 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
Similar Questions
A spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released , what is
(a) the speed of the mass when the spring is compressed by 1.0cm?
Potential energy of the mass when it momentarily comed to rest ?
(c) Total energy of the oscillating mass.

View SolutionA mass of 5 kg is attached to the free end of a spring pulled sideways to a distance of 3 cm and released. What will be the

(a) Speed of this mass when spring is compressed by 2 cm ?
(b) Potential energy of the mass at the point where kinetic energy becomes zero ?
View Solution
Knowledge Check
A spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring,pulled sideways to a distance of 2 cm and released . The speed of the mass when the spring is compressed by 1 cm is
A0.175ms−1B0.35ms−1C0.7ms−1D1.4ms−1A spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring, pulled sideways to a distance of 2 cm and released .P.E. of the mass when it momentarily comes to rest and total energy are
A0.12J,0B0,0.12JC0,0D0.12J,0.12JTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mk
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
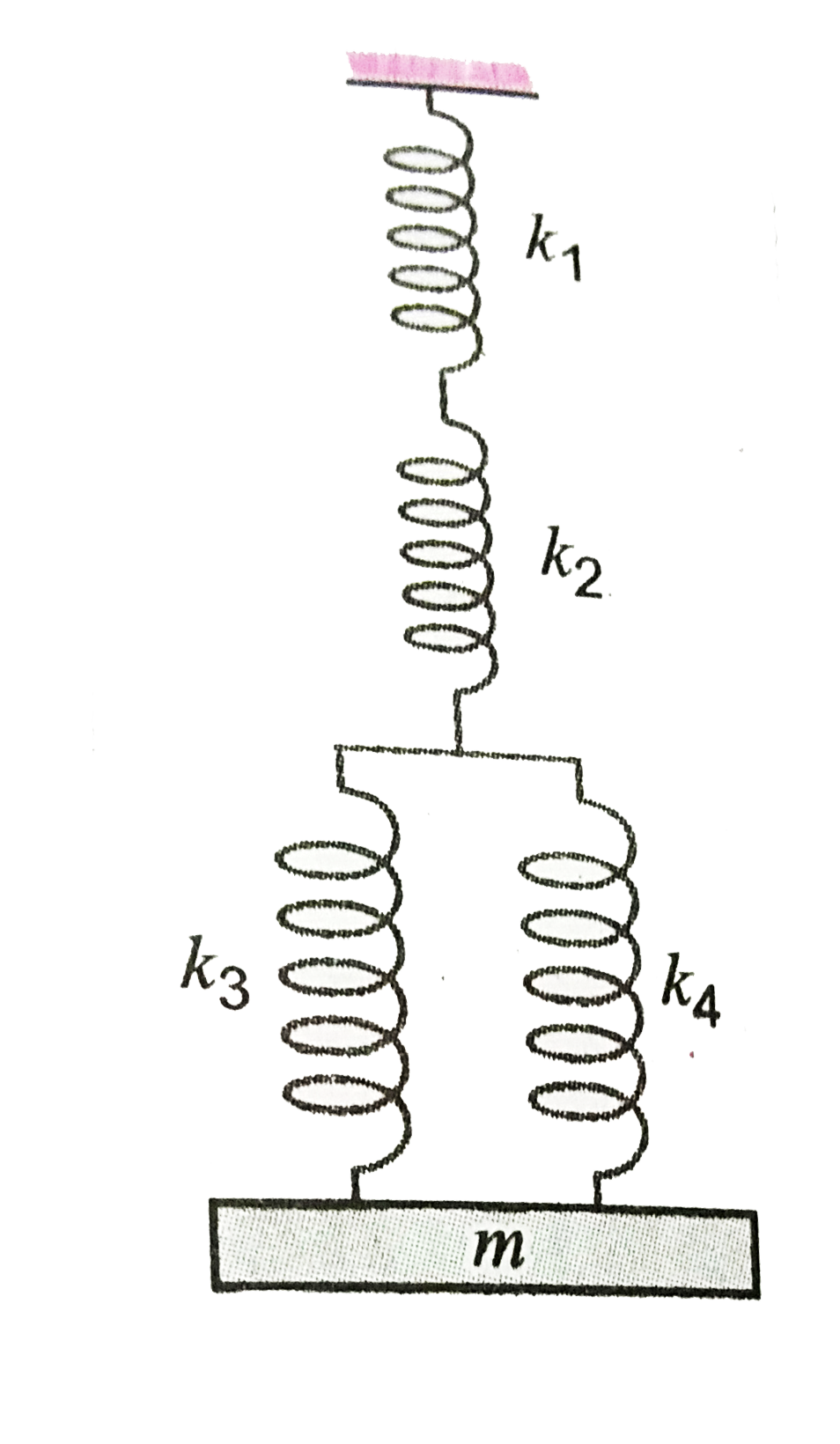
View SolutionTwo bodies of masses 1 kg and 3 kg respectively are connected rigidly by a vertcal spring. The body of mass 3 kg rests on a smototh horizontal surface. The force constant of the spring is 484Nm−1. From the equilibrium position, the mass of 1 kg is displaced vertically through a distance of 0.02 m and then released. calculate (i) and frequency of oscillation of the mass of 1 kg (ii) the maximum velocity of this mass (iii) its oscillation energy and (iv) the reaction of the table on the mass of 3 kg, when mass 1 kg is having harmonic oscillations.
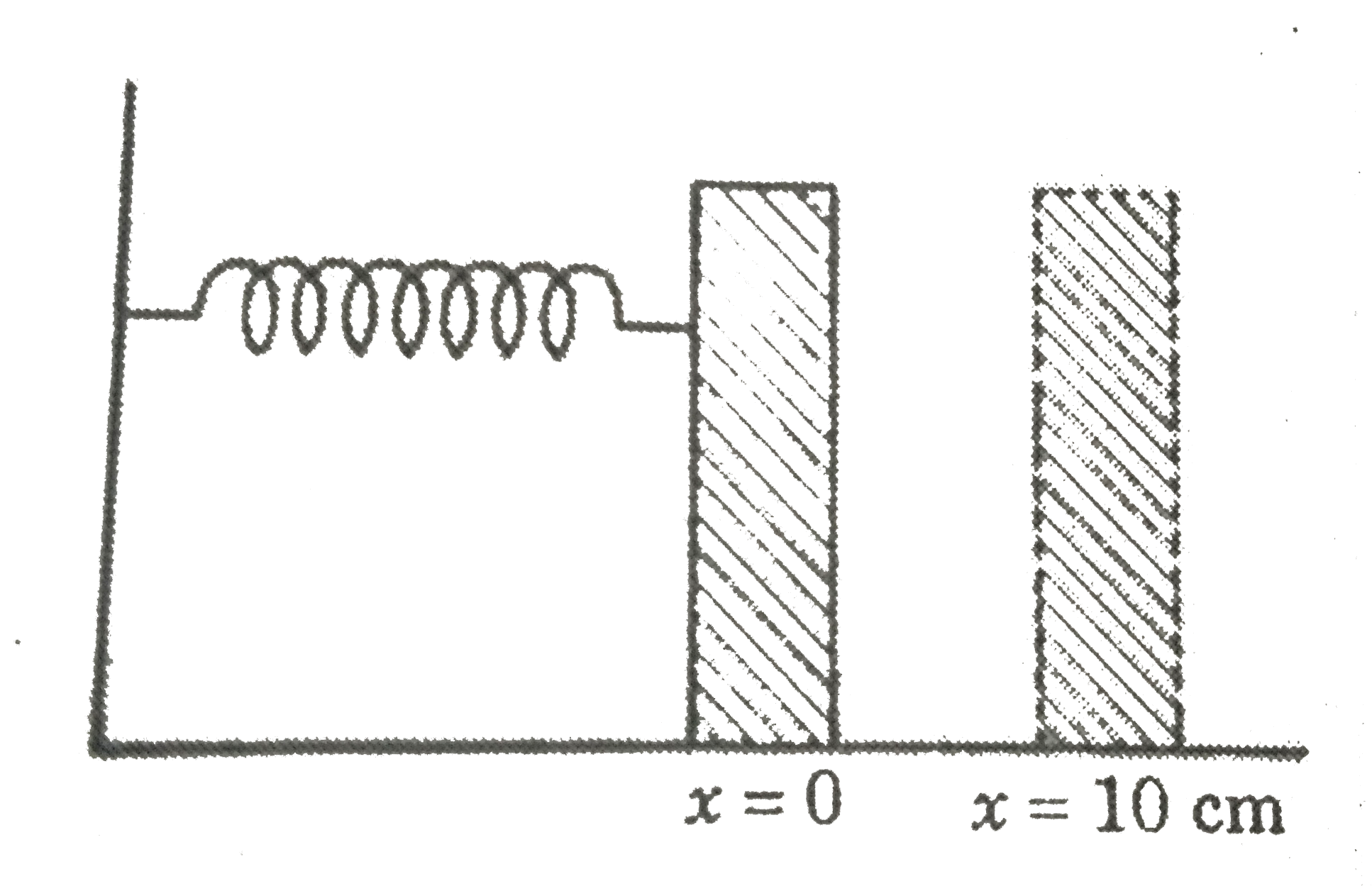
View SolutionTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View SolutionA weightless spring of length 60 cm and force constant 100Nm−1 is kept straight and unstretched on a smooth horizontal table and its ends are rigidly fixed. A mass of 0.25 kg is attached at the middle of the spring and is slightly displaced along the length. The time period of the oscillation of the mass is
View SolutionA weightless spring of length 60 cm and force constant 200 N/m is kept straight and unstretched on a smooth horizontal table and its ends are rigidly fixed. A mass of 0.25 kg is attached at the middle of the spring and is slightly displaced along the length. The time period of the oscillation of the mass is
View Solution